题目内容
2．
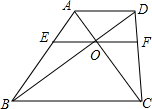已知：如图，梯形ABCD中，AD∥BC，AC、BD交于点O，EF经过点O且和两底平行，交AB于E，交CD于F，求证：OE=OF．
分析 由梯形ABCD中，AD∥BC，EF经过点O且和两底平行，易得△AOD∽△COB，△AEO∽△ABC，△DOF∽△DBC，然后由相似三角形的对应边成比例，证得结论．
解答 证明：∵梯形ABCD中，AD∥BC，
∴△AOD∽△COB，
∴OA：OC=OA：OB，
∴OA：AC=OD：BD，
∵EF∥BC，
∴△AEO∽△ABC，△DOF∽△DBC，
∴OE：BC=OA：AC，OF：BC=OD：BD，
∴OE：BC=OF：BC，
∴OE=OF．
点评 此题考查了相似三角形的判定与性质．注意证得△AOD∽△COB，△AEO∽△ABC，△DOF∽△DBC是关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知y关于x的一次函数y=（2m2-32）x3-（n-3）x2+（m-n）x+m+n．
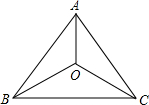如图，在△ABC中，AB=AC．BO=CO．求证：AO⊥BC．
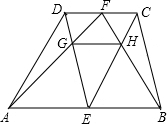如图，梯形ABCD中，AB∥CD，AB=m，CD=n，E、F分别是AB、CD的中点，AF、ED相交于点G，BF、CE相交于点H，则GH=$\frac{mn}{m+n}$．