题目内容
12.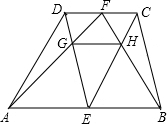 如图,梯形ABCD中,AB∥CD,AB=m,CD=n,E、F分别是AB、CD的中点,AF、ED相交于点G,BF、CE相交于点H,则GH=$\frac{mn}{m+n}$.
如图,梯形ABCD中,AB∥CD,AB=m,CD=n,E、F分别是AB、CD的中点,AF、ED相交于点G,BF、CE相交于点H,则GH=$\frac{mn}{m+n}$.
分析 先由AB∥CD,得到△DFG和△EAG、△CFH△和△EBH的相似关系,从而得到FG和GA、FH和HB间的比例关系,进而得到△GFH和△AFB间关系,利用比例表示出GH的长.
解答 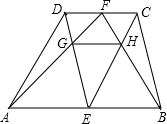 解:∵AB=m,CD=n,E、F分别是AB、CD的中点,
解:∵AB=m,CD=n,E、F分别是AB、CD的中点,
∴DF=FC=$\frac{1}{2}$n,AE=BE=$\frac{1}{2}$m.
∵AB∥CD,
∴△DFG∽△EAG,△CFH∽△EBH,
∴$\frac{FG}{GA}=\frac{DF}{AE}=\frac{n}{m}$,$\frac{FH}{HB}=\frac{FC}{EB}=\frac{n}{m}$.
∴$\frac{FG}{GA}=\frac{FH}{HB}=\frac{n}{m},\frac{FG}{AF}=\frac{FH}{FB}=\frac{n}{m+n}$,
又∵∠GFH=∠AFB,
∴△GFH∽△AFB,
∴$\frac{GH}{AB}=\frac{FG}{FA}$∴$\frac{GH}{m}=\frac{n}{m+n}$,∴$GH=\frac{mn}{m+n}$.
点评 本题考查了相似三角形的性质和判定,利用了比例的性质.定理“两边对应成比例,夹角相等的两个三角形相似”,用的较少.容易想不到.

练习册系列答案
相关题目
7. 如图,△ABC中,AB=AC,D为BC中点,在BA的延长线上取一点E,使得ED=EC,ED与AC交于点F,则$\frac{AF}{CF}$的值为( )
如图,△ABC中,AB=AC,D为BC中点,在BA的延长线上取一点E,使得ED=EC,ED与AC交于点F,则$\frac{AF}{CF}$的值为( )
 如图,△ABC中,AB=AC,D为BC中点,在BA的延长线上取一点E,使得ED=EC,ED与AC交于点F,则$\frac{AF}{CF}$的值为( )
如图,△ABC中,AB=AC,D为BC中点,在BA的延长线上取一点E,使得ED=EC,ED与AC交于点F,则$\frac{AF}{CF}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
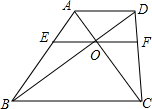 已知:如图,梯形ABCD中,AD∥BC,AC、BD交于点O,EF经过点O且和两底平行,交AB于E,交CD于F,求证:OE=OF.
已知:如图,梯形ABCD中,AD∥BC,AC、BD交于点O,EF经过点O且和两底平行,交AB于E,交CD于F,求证:OE=OF. 如图,为测量小河的宽度,先在河岸边任取一点A,再在河的另一岸边取两点B,C,测得∠ABC=60°,∠ACB=30°,量得BC的长为20m,AB的长为BC长的一半,求小河的宽度.(结果保留根号)
如图,为测量小河的宽度,先在河岸边任取一点A,再在河的另一岸边取两点B,C,测得∠ABC=60°,∠ACB=30°,量得BC的长为20m,AB的长为BC长的一半,求小河的宽度.(结果保留根号) 如图,AE平分∠BAC交BC于点D,∠C=∠EBC,∠BAC=70°,∠ABC=30°,求∠E和∠ADC的度数.
如图,AE平分∠BAC交BC于点D,∠C=∠EBC,∠BAC=70°,∠ABC=30°,求∠E和∠ADC的度数. 如图,已知矩形ABCD中,AB=4,AD=3,P是以CD为直径的半圆上的一个动点,连接BP,则BP的最大值是$\sqrt{13}$+2.
如图,已知矩形ABCD中,AB=4,AD=3,P是以CD为直径的半圆上的一个动点,连接BP,则BP的最大值是$\sqrt{13}$+2. 在正方形ABCD中,P为AB的中点,BE⊥PD的延长线于点E,连接AE、BE、FA⊥AE交DP于点F,连接BF,FC.求证下列结论:
在正方形ABCD中,P为AB的中点,BE⊥PD的延长线于点E,连接AE、BE、FA⊥AE交DP于点F,连接BF,FC.求证下列结论: