题目内容
12.若(x2+y2)(x2+4+y2)-21=0,则x2+y2=3.分析 设t=x2+y2,则原方程化为t(t+4)-21=0,再利用因式分解法解方程得t1=-7,t2=3,利用非负数的性质可得到x2+y2=3.
解答 解:设t=x2+y2,则原方程化为t(t+4)-21=0,
整理得t2+4t-21=0,
解得t1=-7,t2=3,
当t=-7时,x2+y2=-7(舍去),
当t=3时,x2+y2=3.
故答案为3.
点评 本题考查了换元法解一元二次方程:我们常用的是整体换元法,是在已知或者未知中,某个代数式几次出现,而用一个字母来代替它从而简化问题,当然有时候要通过变形才能发现.把一些形式复杂的方程通过换元的方法变成一元二次方程,从而达到降次的目的.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
1. 如图,△ABC的平分线AD与中线BE交于点O,有结论( )
如图,△ABC的平分线AD与中线BE交于点O,有结论( )
①AO是△ABE的角平分线;②BO是△ABD的中线.
 如图,△ABC的平分线AD与中线BE交于点O,有结论( )
如图,△ABC的平分线AD与中线BE交于点O,有结论( )①AO是△ABE的角平分线;②BO是△ABD的中线.
| A. | ①、②都正确 | B. | ①不正确,②正确 | C. | ①、②都不正确 | D. | ①正确,②不正确 |
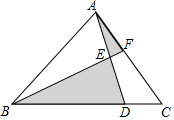 三角形ABC的面积为10cm2,AE=$\frac{1}{2}$AD,BD=3DC,求阴影部分的面积.
三角形ABC的面积为10cm2,AE=$\frac{1}{2}$AD,BD=3DC,求阴影部分的面积.