题目内容
4.已知函数式的x范围,求y范围:(可结合草图求解)(1)已知二次函数y=x2在2<x<3范围内,求y的范围;
(2)已知二次函数y=-x2+4在-2<x<3范围内,求y的范围.
分析 利用配方法把二次函数化为顶点式,即可得出其对称轴方程及顶点坐标;根据x、y轴上点的坐标特点分别另y=0求出x的值,令x=0求出y的值,进而解答即可.
解答 解:(1)y=x2=(x-0)2+0;
∴x=0时,该函数取最小值0;
所以2<x<3,y的范围为4<y<9;
(2)y=-x2+4=-(x-0)2+4;
∴x=0时,该函数取最大值4;
所以-2<x<3,y的范围为-5<y<4.
点评 本题考查的是二次函数的性质、抛物线与x轴的交点及配方法的应用,熟知以上知识是解答此题的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
13.某校为了做好大课间活动,计划用400元购买10件体育用品,备选体育用品及单价如下表(单位:元)
若400元全部用来购买篮球和羽毛球拍共10件,问篮球和羽毛球拍各购买多少件?
| 备选体育用品 | 篮球 | 排球 | 羽毛球拍 |
| 单价(元) | 50 | 40 | 25 |
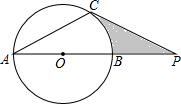 已知如图,⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.
已知如图,⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP. 如图,线段AC、BD交于点O,AB=CD且AB∥CD,点E、F在线段AC上,且AF=CE.求证:FD=BE.
如图,线段AC、BD交于点O,AB=CD且AB∥CD,点E、F在线段AC上,且AF=CE.求证:FD=BE. =-10,
=-10, =4,
=4, =1的规律.求:
=1的规律.求: 的值为-8.
的值为-8.