题目内容
5.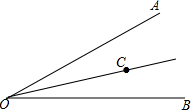 如图,OC平分∠AOB.
如图,OC平分∠AOB.①在图中画出表示点C到OA,OB距离的线段CM,CN并比较CM,CN的大小.
②在OC上另选一点C′,画出标识点C′到OA,OB距离的线段CM′,CN′,再比较C′M′和C′N′的大小.
③试根据①和②猜想,可以得到结论,试用你自己的语言叙述出来.
分析 ①过点C分别作CM⊥OA于M,CN⊥OB于N,则CM=CN;
②过点C分别作C′M′⊥OA于M′,C′N′⊥OB于N,则C′M′=C′N′;
③结论表述为角平分线的性质定理.
解答 解:①如图,CM、CN为所作,
CM=CN;
②如图,C′M′、C′N′为所作,
CM′=CN′;
③结论为:角的平分线上的点到角的两边的距离相等.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
相关题目
13.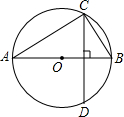 如图所示,已知AB是⊙O的直径,弦CD⊥AB,AC=2$\sqrt{2}$,BC=1,那么CD的值是( )
如图所示,已知AB是⊙O的直径,弦CD⊥AB,AC=2$\sqrt{2}$,BC=1,那么CD的值是( )
 如图所示,已知AB是⊙O的直径,弦CD⊥AB,AC=2$\sqrt{2}$,BC=1,那么CD的值是( )
如图所示,已知AB是⊙O的直径,弦CD⊥AB,AC=2$\sqrt{2}$,BC=1,那么CD的值是( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{2}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
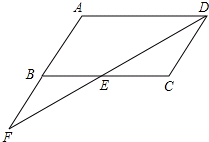 如图.在平行四边形ABCD中,点F在AB的延长线上,且BF=AB.连接FD,交BC于点E
如图.在平行四边形ABCD中,点F在AB的延长线上,且BF=AB.连接FD,交BC于点E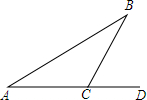 如图,一艘船沿着AC的方向以50海里/小时的速度航行,在A点测得∠BAD=30°,4个小时后到达C点,在C点测得∠BCD=60°.
如图,一艘船沿着AC的方向以50海里/小时的速度航行,在A点测得∠BAD=30°,4个小时后到达C点,在C点测得∠BCD=60°.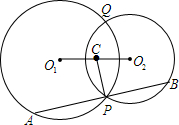 己知:如图.⊙01与⊙O2相交于点P、Q.点C是线段O1O2的中点,AB过点P且与CP垂直,点A、B分别是AB与⊙O1、⊙O2的交点,求证:AP=BP.
己知:如图.⊙01与⊙O2相交于点P、Q.点C是线段O1O2的中点,AB过点P且与CP垂直,点A、B分别是AB与⊙O1、⊙O2的交点,求证:AP=BP.