题目内容
16.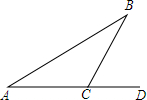 如图,一艘船沿着AC的方向以50海里/小时的速度航行,在A点测得∠BAD=30°,4个小时后到达C点,在C点测得∠BCD=60°.
如图,一艘船沿着AC的方向以50海里/小时的速度航行,在A点测得∠BAD=30°,4个小时后到达C点,在C点测得∠BCD=60°.(1)求BC两点的距离.
(2)已知B周围150海里范用内有暗礁,问沿现在的航线继续航行有没有危险,为什么?(参考数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.732)
分析 (1)过B作BE⊥AC于点E,根据方向角的定义及三角形外角的性质求出∠ABC=∠A=30°,那么根据等角对等边得到BC=AC=200海里;
(2)在Rt△BCE中,由∠BCE=60°,利用三角函数的知识求得BE的长,又由B周围150海里范围内有暗礁,比较BE与150的大小,即可得沿现在的航线继续航行有没有危险.
解答  解:(1)如图,过B作BE⊥AC于点E.
解:(1)如图,过B作BE⊥AC于点E.
∵一艘船沿着AC的方向以50海里/小时的速度航行,4个小时后到达C点,
∴AC=50×4=200(海里).
在Rt△CBE中,∠BCE=60°,
在Rt△ABC中,∠A=30°,
∵∠BCE=∠A+∠ABC=60°,
∴∠ABC=∠A=30°,
∴BC=AC=200海里,
即B、C两点的距离为200海里;
(2)沿现在的航线继续航行有没有危险.理由如下:
在直角△BCE中,∵∠BCE=60°,
∴BE=BC•sin∠BCE=200×$\frac{\sqrt{3}}{2}$=100$\sqrt{3}$≈173.2(海里).
∵150<100$\sqrt{3}$,
∴沿现在的航线继续航行没有危险.
点评 此题主要考查了解直角三角形的应用-方向角问题,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,四边形ABCD中,∠C=∠D=90°,以AB为直径的⊙O与边CD切于点E,与BC交于点F.
如图,四边形ABCD中,∠C=∠D=90°,以AB为直径的⊙O与边CD切于点E,与BC交于点F. 如图是正方体的表面展开图,你能说出图中的各种颜色在正方体中与它相对面上的颜色吗?不妨试一试.
如图是正方体的表面展开图,你能说出图中的各种颜色在正方体中与它相对面上的颜色吗?不妨试一试.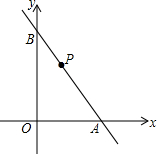 如图所示,已知直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于A,B两点,点P是线段AB上的一个动点,连结OP,把△ABO分成两个小三角形,分别是△AOP和△BOP,当AP的长为多少时,△AOP和△BOP中至少有一个是等腰三角形?
如图所示,已知直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于A,B两点,点P是线段AB上的一个动点,连结OP,把△ABO分成两个小三角形,分别是△AOP和△BOP,当AP的长为多少时,△AOP和△BOP中至少有一个是等腰三角形? (1)在图中,以点P为位似中心,按相似比2:1将图形放大;
(1)在图中,以点P为位似中心,按相似比2:1将图形放大;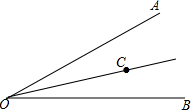 如图,OC平分∠AOB.
如图,OC平分∠AOB.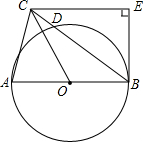 如图,△ABC中,AB=BC,以AB为直径的⊙O交BC于D,BE与⊙O切于点B,且CE⊥BE.
如图,△ABC中,AB=BC,以AB为直径的⊙O交BC于D,BE与⊙O切于点B,且CE⊥BE.