题目内容
10.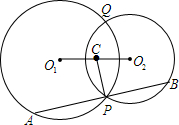 己知:如图.⊙01与⊙O2相交于点P、Q.点C是线段O1O2的中点,AB过点P且与CP垂直,点A、B分别是AB与⊙O1、⊙O2的交点,求证:AP=BP.
己知:如图.⊙01与⊙O2相交于点P、Q.点C是线段O1O2的中点,AB过点P且与CP垂直,点A、B分别是AB与⊙O1、⊙O2的交点,求证:AP=BP.
分析 作O1D⊥AP于点D,O2E⊥BP于点E,分别运用垂径定理得到AP=2PD,BP=2PE,求出PD=PE即可.
解答 证明:分别作O1D⊥AP于点D,O2E⊥BP于点E,
则AP=2PD,BP=2PE.
∵O1D⊥AP,O2E⊥BP,
∴O1D∥PC∥O2E,
∵C为O1O2的中点,
∴PD=PE,
∴AP=BP.
点评 本题考查了相交两圆的性质,垂径定理的应用,能根据相交两圆的性质得出AP=2PD和BP=2PE是解此题的关键,注意:相交两圆的连心线垂直平分公共弦.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
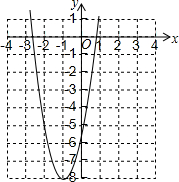 这是小明在阅读一本关于函数的课外读物时看到的一段文字:“由图象知,当x=-1时,二次函数y=ax2+6x-5的值最小”,你能写出a的值吗?
这是小明在阅读一本关于函数的课外读物时看到的一段文字:“由图象知,当x=-1时,二次函数y=ax2+6x-5的值最小”,你能写出a的值吗?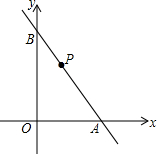 如图所示,已知直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于A,B两点,点P是线段AB上的一个动点,连结OP,把△ABO分成两个小三角形,分别是△AOP和△BOP,当AP的长为多少时,△AOP和△BOP中至少有一个是等腰三角形?
如图所示,已知直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于A,B两点,点P是线段AB上的一个动点,连结OP,把△ABO分成两个小三角形,分别是△AOP和△BOP,当AP的长为多少时,△AOP和△BOP中至少有一个是等腰三角形?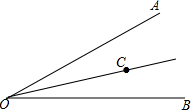 如图,OC平分∠AOB.
如图,OC平分∠AOB.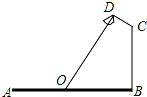 如图,要在宽为22米的大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,求路灯的灯柱BC高度.
如图,要在宽为22米的大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,求路灯的灯柱BC高度.