题目内容
若|x-1|+(y+2)2+
=0,则x+y+z= .
| z-3 |
考点:非负数的性质:算术平方根,非负数的性质:绝对值,非负数的性质:偶次方
专题:
分析:根据非负数的性质列式求出x、y、z,然后代入代数式计算即可得解.
解答:解:由题意得,x-1=0,y+2=0,z-3=0,
解得x=1,y=-2,z=3,
所以,x+y+z=1-2+3=2.
故答案为:2.
解得x=1,y=-2,z=3,
所以,x+y+z=1-2+3=2.
故答案为:2.
点评:本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
相关题目
 一只跳蚤在第一象限及x轴,y轴上跳动,在第一秒钟,它从跳点跳动到(0,1),然后继续按图中箭头所示方向跳动即(0,0)→(0,1)→(1,1)→(1,0)→…1,且每秒跳动一个单位.那么第35秒时跳蚤所在位置的坐标是( )
一只跳蚤在第一象限及x轴,y轴上跳动,在第一秒钟,它从跳点跳动到(0,1),然后继续按图中箭头所示方向跳动即(0,0)→(0,1)→(1,1)→(1,0)→…1,且每秒跳动一个单位.那么第35秒时跳蚤所在位置的坐标是( )| A、(5,0) |
| B、(4,0) |
| C、(0,5) |
| D、(5,5) |
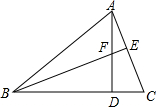 △ABC中,∠C=60°,高BE经过高AD的中点F,EF=1,则BF长为( )
△ABC中,∠C=60°,高BE经过高AD的中点F,EF=1,则BF长为( )| A、2 | B、3 | C、4 | D、5 |
 如图,四边形ABCD的顶点都在⊙O上,点O在四边形内部,若四边形OABC为平行四边形,则∠D等于( )
如图,四边形ABCD的顶点都在⊙O上,点O在四边形内部,若四边形OABC为平行四边形,则∠D等于( )| A、30° | B、45° |
| C、60° | D、不能确定 |
函数值y随x的增大而减小的是( )
| A、y=1+x | ||
B、y=
| ||
| C、y=-x+1 | ||
| D、y=-2+3x |
 如图所示,图中平行四边形的一个角为60°,两条边的长分别为6cm和12cm,高为5cm.求图中阴影部分的面积.
如图所示,图中平行四边形的一个角为60°,两条边的长分别为6cm和12cm,高为5cm.求图中阴影部分的面积.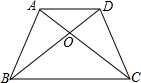 等腰梯形ABCD中,AD∥BC,AB=CD,对角线AC、BD交于点O,AC=2,∠BOC=120°,求AD+BC的值.
等腰梯形ABCD中,AD∥BC,AB=CD,对角线AC、BD交于点O,AC=2,∠BOC=120°,求AD+BC的值. a,b为有理数,它们表示的点在数轴上的位置如图:
a,b为有理数,它们表示的点在数轴上的位置如图: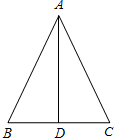 如图,在△ABC中,AB=13,BC=10,BC边上的中线AD=12.
如图,在△ABC中,AB=13,BC=10,BC边上的中线AD=12.