题目内容
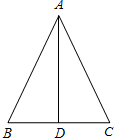 如图,在△ABC中,AB=13,BC=10,BC边上的中线AD=12.
如图,在△ABC中,AB=13,BC=10,BC边上的中线AD=12.(1)AD平分∠BAC吗?请说明理由.
(2)求:△ABC的面积.
考点:勾股定理
专题:
分析:(1)先根据BC为斜边上的中线求出BD的长,再由勾股定理的逆定理判断出△ABD的形状,故可得出△ABC是等腰三角形,根据等腰三角形三线合一的性质即可得出结论;
(2)由(1)可知△ABC是等腰三角形,再根据三角形的面积公式即可得出结论.
(2)由(1)可知△ABC是等腰三角形,再根据三角形的面积公式即可得出结论.
解答:解:(1)AD平分∠BAC.
理由:∵BC为斜边上的中线,
∴BD=5.
∵在△ABC中,AB=13,AD=12,BD=5,
∴132=122+52,即AB2=AD2+BD2,
∴∠ADB=90°,即AD⊥BC,
∴AD垂直平分BC,
∴AB=AC,
∴AD平分∠BAC;
(2)∵由(1)知,△ABC是等腰三角形,
∴BC=2BD=5,
∴S△ABC=
BC•AD=
×10×12=60.
理由:∵BC为斜边上的中线,
∴BD=5.
∵在△ABC中,AB=13,AD=12,BD=5,
∴132=122+52,即AB2=AD2+BD2,
∴∠ADB=90°,即AD⊥BC,
∴AD垂直平分BC,
∴AB=AC,
∴AD平分∠BAC;
(2)∵由(1)知,△ABC是等腰三角形,
∴BC=2BD=5,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
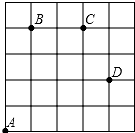 如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向. 如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是( )
如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是( )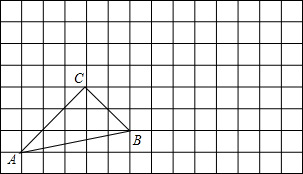 如图,在一个边长为1的正方形网格上,把△ABC向右平移4个方格,再向上平移2个方格,得到△A′B′C′(A′、B′、C′分别对应A、B、C).
如图,在一个边长为1的正方形网格上,把△ABC向右平移4个方格,再向上平移2个方格,得到△A′B′C′(A′、B′、C′分别对应A、B、C). 如图所示的几何体是由一个正方体切去一个小正方体形成的,从正面看到的平面图形为( )
如图所示的几何体是由一个正方体切去一个小正方体形成的,从正面看到的平面图形为( )


