题目内容
 如图,四边形ABCD的顶点都在⊙O上,点O在四边形内部,若四边形OABC为平行四边形,则∠D等于( )
如图,四边形ABCD的顶点都在⊙O上,点O在四边形内部,若四边形OABC为平行四边形,则∠D等于( )| A、30° | B、45° |
| C、60° | D、不能确定 |
考点:圆周角定理,平行四边形的性质
专题:
分析:先根据平行四边形的性质得出∠B=∠AOC,再由圆周角定理得出∠D=
∠AOC,由圆内接四边形的性质得出∠D+∠ABC=180°,由此可得出结论.
| 1 |
| 2 |
解答:解:∵四边形OABC为平行四边形,
∴∠B=∠AOC,
∵∠D=
∠AOC,
∴2∠D=∠B.
∵四边形ABCD是圆内接四边形,
∴∠D+∠B=180°,即3∠D=180°,解得∠D=60°.
故选C.
∴∠B=∠AOC,
∵∠D=
| 1 |
| 2 |
∴2∠D=∠B.
∵四边形ABCD是圆内接四边形,
∴∠D+∠B=180°,即3∠D=180°,解得∠D=60°.
故选C.
点评:本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
相关题目
 如图,□ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
如图,□ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )| A、3cm | B、6cm |
| C、9cm | D、12cm |
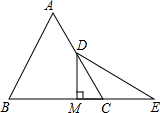 如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M.
如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M. 已知a、b、c为有理数,且它们在数轴上的位置如图所示.
已知a、b、c为有理数,且它们在数轴上的位置如图所示. 如图,?ABCD中,E是BC的中点,AE=9,BD=12,AD=10.
如图,?ABCD中,E是BC的中点,AE=9,BD=12,AD=10. 如图,若圆心角∠AOB=110°,则圆周角∠ADB=
如图,若圆心角∠AOB=110°,则圆周角∠ADB= 在数轴上表示下列各数:0,1.5,3,
在数轴上表示下列各数:0,1.5,3,