题目内容
6.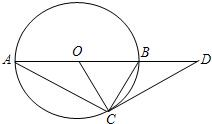 如图,AB是⊙O的直径,∠A=30°,延长OB到D,使BD=OB.
如图,AB是⊙O的直径,∠A=30°,延长OB到D,使BD=OB.(1)△OBC是等边三角形.
(2)求证:DC是⊙O的切线.
分析 (1)由圆周角定理可求得∠BOC=60°,然后依据有一个角是60°的等腰三角形是等边三角形进行判断即可;
(2)由等边三角形的性质可求得∠OCB=∠OBC=60°,然后可求得∠BCD=30°,从而可证明OC⊥CD.
解答 解:(1)∵∠A=30°,
∴∠BOC=60°.
又∵OB=OC,
∴△OBC是等边三角形.
故答案为:等边.
(2)∵△OBC是等边三角形,
∴∠OCB=∠OBC=60°.
∵BC=BD,
∴∠BCD=∠BDC.
又∵∠BOC=∠BCD+∠BDC=60°,
∴∠BCD=30°.
∴∠OCD=∠OCB+∠BCD=60°+30°=90°.
点评 本题主要考查的是切线的判定、圆周角定理的应用、等腰三角形的性质、等边三角形的性质和判定,熟练掌握相关性质是解题的关键.

练习册系列答案
相关题目
11.一枚质地均匀的正方体骰子六个面上的数字分别为1,2,3,4,5,6.掷四次骰子,依次得到朝上的面上的数字分别为a,b,c,d,则在a,a+b,a+b+c,a+b+c+d中存在一个数等于4的概率为( )
| A. | $\frac{33}{1296}$ | B. | $\frac{334}{1296}$ | C. | $\frac{343}{1296}$ | D. | $\frac{433}{1296}$ |
18. 如图,AB、AC是⊙O的两条弦,∠A=30°,过点C的切线与OB的延长线交于点D,则∠D的度数为( )
如图,AB、AC是⊙O的两条弦,∠A=30°,过点C的切线与OB的延长线交于点D,则∠D的度数为( )
 如图,AB、AC是⊙O的两条弦,∠A=30°,过点C的切线与OB的延长线交于点D,则∠D的度数为( )
如图,AB、AC是⊙O的两条弦,∠A=30°,过点C的切线与OB的延长线交于点D,则∠D的度数为( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
16.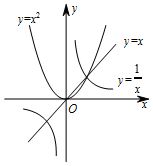 给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象
给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象
①如果$\frac{1}{a}$>a>a2,那么0<a<1;
②如果a2>a>$\frac{1}{a}$,那么a>1;
③如果$\frac{1}{a}$>a2>a,那么-1<a<0;
④如果a2>$\frac{1}{a}$>a时,那么a<-1.
则( )
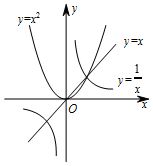 给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象
给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象①如果$\frac{1}{a}$>a>a2,那么0<a<1;
②如果a2>a>$\frac{1}{a}$,那么a>1;
③如果$\frac{1}{a}$>a2>a,那么-1<a<0;
④如果a2>$\frac{1}{a}$>a时,那么a<-1.
则( )
| A. | 正确的命题是①④ | B. | 错误的命题是②③④ | C. | 正确的命题是①② | D. | 错误的命题只有③ |
 如图,在四边形ABCD中,∠B=90°,DE∥AB,DE交BC于E,交AC于F,DE=BC,∠CDE=∠ACB=30°.
如图,在四边形ABCD中,∠B=90°,DE∥AB,DE交BC于E,交AC于F,DE=BC,∠CDE=∠ACB=30°. 如图,I为△ABC的角平分线交点,∠A=40°,则∠BIC的度数是110°.
如图,I为△ABC的角平分线交点,∠A=40°,则∠BIC的度数是110°.