题目内容
11.一枚质地均匀的正方体骰子六个面上的数字分别为1,2,3,4,5,6.掷四次骰子,依次得到朝上的面上的数字分别为a,b,c,d,则在a,a+b,a+b+c,a+b+c+d中存在一个数等于4的概率为( )| A. | $\frac{33}{1296}$ | B. | $\frac{334}{1296}$ | C. | $\frac{343}{1296}$ | D. | $\frac{433}{1296}$ |
分析 根据题意得出当a=4时,共有6×6×6=216种可能结果;当a+b=4,即第1、2次抛掷的结果分别为1、3或2、2或3、1时,其结果数为6×6+6×6+6×6=108种;当a+b+c=4时,即第1、2、3次抛掷的结果分别为1、1、2或1、2、1或2、1、1时,其结果数为6+6+6=18种;当a+b+c+d=4时,即第1、2、3、4抛掷的结果均为1点,其结果数只有1种,根据概率公式求解可得.
解答 解:抛掷一枚质地均匀的正方体骰子四次共有6×6×6×6=1296种等可能结果,
依次得到朝上的面上的数字分别为a,b,c,d,
当a=4时,此时共有6×6×6=216种可能结果,
当a+b=4,即第1、2次抛掷的结果分别为1、3或2、2或3、1时,其结果数为6×6+6×6+6×6=108种,
当a+b+c=4时,即第1、2、3次抛掷的结果分别为1、1、2或1、2、1或2、1、1时,其结果数为6+6+6=18种,
当a+b+c+d=4时,即第1、2、3、4抛掷的结果均为1点,其结果数只有1种,
综上,在a,a+b,a+b+c,a+b+c+d中存在一个数等于4的共有216+108+18+1=343,
则在a,a+b,a+b+c,a+b+c+d中存在一个数等于4的概率为$\frac{343}{1296}$,
故选:C.
点评 本题主要考查列表法或树状图法求概率,根据题意得出a,a+b,a+b+c,a+b+c+d中存在一个数等于4的结果数是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1. 如图,AB=AC,BD=CD.若∠B=70°,则∠BAC=( )
如图,AB=AC,BD=CD.若∠B=70°,则∠BAC=( )
 如图,AB=AC,BD=CD.若∠B=70°,则∠BAC=( )
如图,AB=AC,BD=CD.若∠B=70°,则∠BAC=( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
19.在同一平面直角坐标系内,将函数y=x2+4x+1的图象沿x轴向右平移2个单位长度后再沿y轴向下平移1个单位长度,得到图象的顶点坐标是( )
| A. | (-1,1) | B. | (0,-4) | C. | (2,-2) | D. | (1,-1) |
3.某单位向一所希望小学赠送1080件文具,现用A,B两种不同的包装箱进行包装,已知每个B型包装箱比A型包装箱多装15件文具,单独使用B型包装箱比单独使用A型包装箱可少用12个,设B型包装箱每个可以装x件文具,根究题意列方程为( )
| A. | $\frac{1080}{x}$=$\frac{1080}{x-15}$-12 | B. | $\frac{1080}{x}$=$\frac{1080}{x-15}$+12 | ||
| C. | $\frac{1080}{x}$=$\frac{1080}{x+15}$-12 | D. | $\frac{1080}{x}$=$\frac{1080}{x+15}$+12 |
 如图,O为直线AB上一点,∠DOE=90°,OD是∠AOC的角平分线,若∠AOC=70°.
如图,O为直线AB上一点,∠DOE=90°,OD是∠AOC的角平分线,若∠AOC=70°.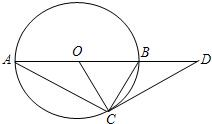 如图,AB是⊙O的直径,∠A=30°,延长OB到D,使BD=OB.
如图,AB是⊙O的直径,∠A=30°,延长OB到D,使BD=OB. 如图,已知四边形ABCD中,∠B=∠C,AB=8,BC=10,CD=3,E是BC上一点,BE=4.
如图,已知四边形ABCD中,∠B=∠C,AB=8,BC=10,CD=3,E是BC上一点,BE=4.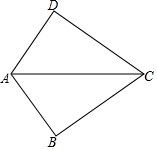 如图,△ABC≌△ADC,∠B=80°,则∠D的度数为80°.
如图,△ABC≌△ADC,∠B=80°,则∠D的度数为80°.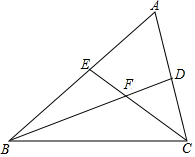 如图,△ABC的∠B和∠C的平分线BD,CE相交于点F,∠A=60°,
如图,△ABC的∠B和∠C的平分线BD,CE相交于点F,∠A=60°,