题目内容
16. 如图,在四边形ABCD中,∠B=90°,DE∥AB,DE交BC于E,交AC于F,DE=BC,∠CDE=∠ACB=30°.
如图,在四边形ABCD中,∠B=90°,DE∥AB,DE交BC于E,交AC于F,DE=BC,∠CDE=∠ACB=30°.(1)若AB=4,求CD的长.
(2)判断△FCD的形状,并说明理由.
分析 (1)证明△ACB≌△CDE,得到AC=CD,根据直角三角形的性质求出AC,求出CD;
(2)根据等腰三角形的判定定理证明.
解答 解:(1)在△ACB和△CDE中,∠B=∠DEC=90°,BC=DE,
∠ACB=∠CDE,
在△ACB和△CDE中,
$\left\{\begin{array}{l}{∠B=∠DEC}\\{BC=DE}\\{∠ACB=∠CDE}\end{array}\right.$,
∴△ACB≌△CDE,
∴AC=CD,
在Rt△ABC中,∠B=90°,∠ACB=30°,AB=4,
∴AC=2AB=8,
∴CD=8;
(2)△FCD是等腰三角形,
理由:∵DE∥AB,∠B=90°,
∴∠DEC=90°,
∴∠DCE=90°-∠CDE=60°,
∴∠DCF=∠DCE-∠ACB=30°,
∴∠CDE=∠DCF,
∴DF=CF,
∴△FCD是等腰三角形.
点评 本题考查的是全等三角形的判定和性质、等腰三角形的判定,掌握全等三角形的判定定理和性质定理是解题的关键.

练习册系列答案
相关题目
11.数据0,1,1,x,3,4的平均数是2,则这组数据的中位数是( )
| A. | 1 | B. | 2 | C. | 2.5 | D. | 3 |
1. 如图,AB=AC,BD=CD.若∠B=70°,则∠BAC=( )
如图,AB=AC,BD=CD.若∠B=70°,则∠BAC=( )
 如图,AB=AC,BD=CD.若∠B=70°,则∠BAC=( )
如图,AB=AC,BD=CD.若∠B=70°,则∠BAC=( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
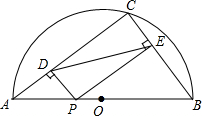 如图,AB是半⊙O的直径,点C是半⊙O上的一点,且AC=4cm,BC=3cm.点P是AB上的动点,过点P分别作PD⊥AC,PE⊥BC,垂足分别为点D、E,连接DE,则在点P移动过程中,DE的最小值为$\frac{12}{5}$cm.
如图,AB是半⊙O的直径,点C是半⊙O上的一点,且AC=4cm,BC=3cm.点P是AB上的动点,过点P分别作PD⊥AC,PE⊥BC,垂足分别为点D、E,连接DE,则在点P移动过程中,DE的最小值为$\frac{12}{5}$cm.



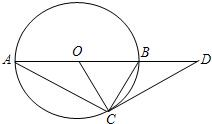 如图,AB是⊙O的直径,∠A=30°,延长OB到D,使BD=OB.
如图,AB是⊙O的直径,∠A=30°,延长OB到D,使BD=OB.