题目内容
3.在△ABC中,AB、BC、AC三边的长分别为$\sqrt{5}$、$\sqrt{10}$、$\sqrt{13}$,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.(1)△ABC的面积为:3.5.
(2)若△DEF三边的长分别为$\sqrt{5}$、$\sqrt{8}$、$\sqrt{17}$,请在图2的正方形网格中画出相应的△DEF,并利用构图法求出它的面积.

分析 (1)利用△ABC所在的正方形的面积减去四周三个小直角三角形的面积,计算即可得解;
(2)根据网格结构和勾股定理作出△DEF,再利用△DEF所在的矩形的面积减去四周三个小直角三角形的面积,计算即可得解.
解答 解:(1)△ABC的面积=3×3-$\frac{1}{2}$×2×1-$\frac{1}{2}$×3×1-$\frac{1}{2}$×2×3,
=9-1-1.5-3,
=9-5.5,
=3.5,
故答案为3.5;
(2)△DEF如图2所示;
面积=2×4-$\frac{1}{2}$×1×2-$\frac{1}{2}$×2×2-$\frac{1}{2}$×1×4,
=8-1-2-2,
=8-5,
=3.
点评 本题考查了勾股定理,构图法求三角形的面积,读懂题目信息,理解构图法的操作方法是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 如图,在数轴上点A、B所表示的数分别为m,n,则m+n符号为正或者“+”.
如图,在数轴上点A、B所表示的数分别为m,n,则m+n符号为正或者“+”.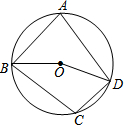 如图,四边形ABCD内接于⊙O,若∠BOD=160°,则∠BCD=100°.
如图,四边形ABCD内接于⊙O,若∠BOD=160°,则∠BCD=100°.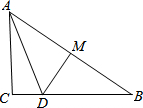 如图,在△ABC中,∠C=90°,AB的垂直平分线交BC于点D,∠CAD:∠DAB=1:2,则∠B的度数为36°.
如图,在△ABC中,∠C=90°,AB的垂直平分线交BC于点D,∠CAD:∠DAB=1:2,则∠B的度数为36°. 如图,反比例函数y=$\frac{18}{x}$的图象过矩形OABC的顶点B,OA、OC分别在x轴、y轴的正半轴上,OA;OC=1:2,矩形OABC的对角线交于点E.
如图,反比例函数y=$\frac{18}{x}$的图象过矩形OABC的顶点B,OA、OC分别在x轴、y轴的正半轴上,OA;OC=1:2,矩形OABC的对角线交于点E.