题目内容
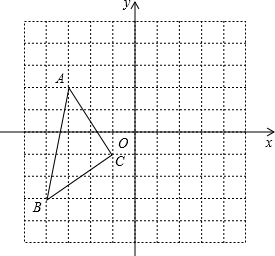 (1)如图,写出点A,B,C的坐标A
(1)如图,写出点A,B,C的坐标A(2)画出△ABC关于y轴对称的△A1B1C1;
(3)写出△ABC关于x轴对称的△A2B2C2的面积
考点:作图-轴对称变换
专题:
分析:(1)利用平面坐标系得出各点坐标即可;
(2)利用关于y轴对称点的坐标性质得出即可;
(3)利用矩形面积减去周围三角形的面积求出即可.
(2)利用关于y轴对称点的坐标性质得出即可;
(3)利用矩形面积减去周围三角形的面积求出即可.
解答: 解:(1)如图所示:A (-3,2),B (-4,-3),C (-1,-1);
解:(1)如图所示:A (-3,2),B (-4,-3),C (-1,-1);
故答案为:(-3,2),B(-4,-3),C(-1,-1);
(2)如图所示:△A1B1C1,即为所求;
(3)△ABC关于x轴对称的△A2B2C2的面积=△ABC的面积
=3×5-
×2×3-
×1×5-
×2×3
=6.5.
故答案为:6.5.
 解:(1)如图所示:A (-3,2),B (-4,-3),C (-1,-1);
解:(1)如图所示:A (-3,2),B (-4,-3),C (-1,-1);故答案为:(-3,2),B(-4,-3),C(-1,-1);
(2)如图所示:△A1B1C1,即为所求;
(3)△ABC关于x轴对称的△A2B2C2的面积=△ABC的面积
=3×5-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=6.5.
故答案为:6.5.
点评:此题主要考查了轴对称变换以及三角形面积求法,得出对应点位置是解题关键.

练习册系列答案
相关题目
李冬坐在教室的第二列第四行,用数对(2,4)来表示,王华坐在第六列第一行,可以用( )来表示.
| A、(1,6) | B、(6,1) |
| C、(0,6) |
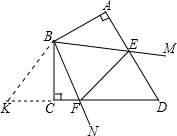 已知四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°,∠MBN=
已知四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°,∠MBN=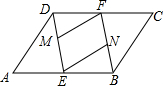 已知在平行四边形ABCD中,AE=CF,点M、N分别是DE、BF的中点,试问ME与FN的数量关系如何?
已知在平行四边形ABCD中,AE=CF,点M、N分别是DE、BF的中点,试问ME与FN的数量关系如何?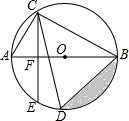 已知AB是⊙O的直径,AB=10cm,弦AC=6cm,弦CE⊥AB,垂足为F,弦CD平分∠ACB.
已知AB是⊙O的直径,AB=10cm,弦AC=6cm,弦CE⊥AB,垂足为F,弦CD平分∠ACB. 如图,在△ABC中,AC=AB,AB的垂直平分线交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16,求△BCF的周长和∠EFC的度数.
如图,在△ABC中,AC=AB,AB的垂直平分线交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16,求△BCF的周长和∠EFC的度数.