题目内容
4.点M(-2,-5)向上平移4个单位后得到的点M′的坐标为( )| A. | (-6,-5) | B. | (2,-5) | C. | (-2,-1) | D. | (-2,-9) |
分析 让点的横坐标不变,纵坐标加4即可.
解答 解:平移后点M的横坐标为-2;纵坐标为-5+4=-1;
∴点P(-2,-5)向上平移4个单位后的点的坐标为(-2,-1).
故选C.
点评 本题考查图形的平移变换,关键是要懂得左右平移点的纵坐标不变,而上下平移时点的横坐标不变.

练习册系列答案
相关题目
14.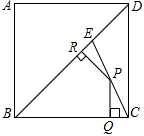 如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是( )
如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是( )
 如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是( )
如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是( )| A. | 2$\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | $\frac{8}{3}$ |
15.一名学生军训时连续射靶10次,命中环数分别为 7,8,6,8,5,9,10,7,6,4.则这名学生射击环数的方差是( )
| A. | 3 | B. | 2.9 | C. | 2.8 | D. | 2.7 |
12.若不等式组$\left\{\begin{array}{l}{x<2m+1}\\{x>7-m}\end{array}\right.$无解,则m的取值范围是( )
| A. | m=2 | B. | m<2 | C. | m≤2 | D. | m≥2 |
9.长方形的周长为60cm,其中一条边为x(其中x>0),面积为ycm2,则在这个长方形中,y与x的关系可以写为( )
| A. | y=60x-2x2 | B. | y=30x-x2 | C. | y=$\frac{1}{2}$x2-60 | D. | y=$\frac{1}{2}$x2-30 |
16.已知x=2是不等式-3(mx-3m+2)≤0的解,且x=1不是这个不等式的解,则实数m的取值范围是( )
| A. | m>1 | B. | m<2 | C. | 1<m≤2 | D. | 1≤m≤2 |
14.将一组数据:3,1,2,4,2,5,4去掉3后,新的数据的特征量发生变化的是( )
| A. | 中位数 | B. | 平均数 | C. | 众数 | D. | 方差 |
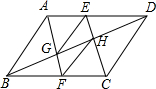 如图,平行四边形ABCD中,点E、F分别是AD、BC的中点,G、H分别是对角线BD上的三等分点.
如图,平行四边形ABCD中,点E、F分别是AD、BC的中点,G、H分别是对角线BD上的三等分点.