题目内容
14.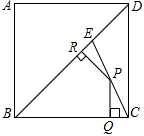 如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是( )
如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是( )| A. | 2$\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | $\frac{8}{3}$ |
分析 连接BP,设点C到BE的距离为h,然后根据S△BCE=S△BCP+S△BEP求出h=PQ+PR,再根据正方形的性质求出h即可.
解答 解:如图,连接BP,设点C到BE的距离为h,
则S△BCE=S△BCP+S△BEP,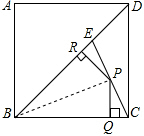
即$\frac{1}{2}$BE•h=$\frac{1}{2}$BC•PQ+$\frac{1}{2}$BE•PR,
∵BE=BC,
∴h=PQ+PR,
∵正方形ABCD的边长为4,
∴h=4×$\frac{\sqrt{2}}{2}$=2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题考查了正方形的性质,三角形的面积,熟记性质并作辅助线,利用三角形的面积求出PQ+PR等于点C到BE的距离是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.若方程组$\left\{\begin{array}{l}{2kx+(k-1)y=3}\\{3x+4y=1}\end{array}\right.$的解x和y互为相反数,则k的值为( )
| A. | -4 | B. | 4 | C. | 2 | D. | -2 |
3.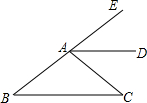 如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠EAC的度数为( )
如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠EAC的度数为( )
 如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠EAC的度数为( )
如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠EAC的度数为( )| A. | 30° | B. | 40° | C. | 60° | D. | 80° |
4.点M(-2,-5)向上平移4个单位后得到的点M′的坐标为( )
| A. | (-6,-5) | B. | (2,-5) | C. | (-2,-1) | D. | (-2,-9) |
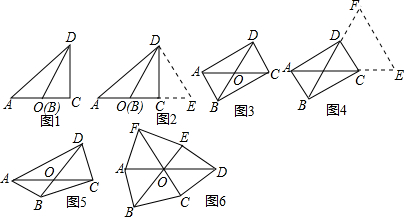
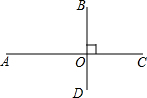 如图,已知线段AC、BD相互垂直,垂足为O,且OA>OC,OB>OD.
如图,已知线段AC、BD相互垂直,垂足为O,且OA>OC,OB>OD.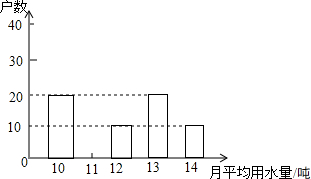 市政府决定对市直机关500户家庭的用水情况作一次调查,调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.
市政府决定对市直机关500户家庭的用水情况作一次调查,调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.