题目内容
10.计算:$\frac{{x}^{2}-1}{{x}^{2}+4x+4}$÷(x+1)•$\frac{{{x^2}+3x+2}}{1-x}$.分析 首先将分子与分母分解因式,进而化简求出答案.
解答 解:原式=$\frac{(x+1)(x-1)}{{{{(x+2)}^2}}}$•$\frac{1}{x+1}$•$\frac{(x+1)(x+2)}{1-x}$
=-$\frac{x+1}{x+2}$.
点评 此题主要考查了分式的乘除运算,正确分解因式是解题关键.

练习册系列答案
相关题目
20.下列的点在第四象限的是( )
| A. | (3,-9) | B. | (2,7) | C. | (-1,6) | D. | (-2,-8) |
1.在有理式$\frac{1}{3}$a-b,$\frac{5}{a},\frac{x+y}{π},\frac{3}{5+y},-\frac{1}{11},\frac{n+p}{m}$中,分式的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
15.函数y=$\frac{2}{\sqrt{3-x}}$自变量的取值范围是( )
| A. | x≥-3 | B. | x<3 | C. | x≤-3 | D. | x≤3 |
20.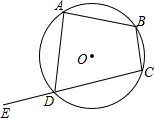 如图,四边形ABCD内接于圆O,E为CD延长线上一点,若∠B=110°,则∠ADE的度数为( )
如图,四边形ABCD内接于圆O,E为CD延长线上一点,若∠B=110°,则∠ADE的度数为( )
 如图,四边形ABCD内接于圆O,E为CD延长线上一点,若∠B=110°,则∠ADE的度数为( )
如图,四边形ABCD内接于圆O,E为CD延长线上一点,若∠B=110°,则∠ADE的度数为( )| A. | 115° | B. | 110° | C. | 90° | D. | 80° |
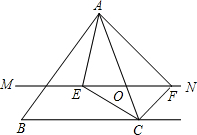 如图,在△ABC中,点O是AC边上(端点除外)的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,连接AE、AF.
如图,在△ABC中,点O是AC边上(端点除外)的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,连接AE、AF.