题目内容
20．
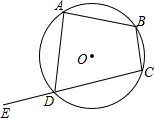如图，四边形ABCD内接于圆O，E为CD延长线上一点，若∠B=110°，则∠ADE的度数为（ ）| A． | 115° | B． | 110° | C． | 90° | D． | 80° |
分析 由四边形ABCD内接于圆O，E为CD延长线上一点，若∠B=110°，根据圆的内接四边形的性质，即可求得∠ADC的度数，继而求得答案．
解答 解：∵四边形ABCD内接于圆O，∠B=110°，
∴∠ADC=180°-∠B=70°，
∴∠ADE=180°-∠ADC=110°．
故选B．
点评 此题考查了圆的内接多边形的性质．注意圆的内接四边形的对角互补．
练习册系列答案
相关题目
若有理数在数轴上的位置如图所示，则化简：|a+c|+|a-b|-|c+a|=a-b．
15．下列各点，在二次函数y=x2-2的图象上的是（ ）
| A． | （0，0） | B． | （-1，-1） | C． | （1，9） | D． | （2，-2） |
如图是一名考古学家发现的一块古代车轮碎片，你能帮他找到这个车轮的半径吗？（画出示意图，保留作图痕迹）
12．把抛物线y=$\frac{1}{2}{x^2}$+1先向右平移1个单位，再向下移2个单位，得到的抛物线解析式是（ ）
| A． | y=$\frac{1}{2}{（{x+1}）^2}$-3 | B． | y=$\frac{1}{2}{（{x-1}）^2}$+3 | C． | y=$\frac{1}{2}{（{x+1}）^2}$-1 | D． | y=$\frac{1}{2}{（{x-1}）^2}$-1 |
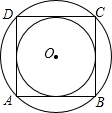求如图正方形的内切圆与外接圆的半径之比．