Question

19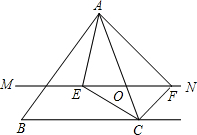．如图，在△ABC中，点O是AC边上（端点除外）的一个动点，过点O作直线MN∥BC．设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F，连接AE、AF．
（1）那么当点O运动到何处时，四边形AECF是矩形？并说明理由．
（2）在（1）的前提下△ABC满足什么条件，四边形AECF是正方形？（直接写出答案，无需证明）

Answer 1

分析 （1）由于CE平分∠BCA，那么有∠1=∠2，而MN∥BC，利用平行线的性质有∠1=∠3，等量代换有∠2=∠3，于OE=OC，同理OC=OF，于是OE=OF，而OA=OC，那么可证四边形AECF是平行四边形，又CE、CF分别是∠BCA及其外角的角平分线，易证∠ECF是90°，从而可证四边形AECF是矩形．
（2）由（1）得出四边形AECF是矩形，再由平行线得出AC⊥EF，得出四边形AECF是菱形，即可得出结论．

解答 （1）解：当点O运动到AC中点时，四边形AECF是矩形；理由如下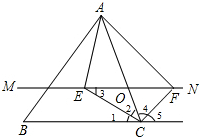：如图所示：
∵CE平分∠BCA，
∴∠1=∠2，
又∵MN∥BC，
∴∠1=∠3，
∴∠3=∠2，
∴EO=CO，
同理，FO=CO，
∴EO=FO，
又∵OA=OC，
∴四边形AECF是平行四边形，
∵CF是∠BCA的外角平分线，
∴∠4=∠5，
又∵∠1=∠2，
∴∠1+∠5=∠2+∠4，
又∵∠1+∠5+∠2+∠4=180°，
∴∠2+∠4=90°，
∴平行四边形AECF是矩形．
（2）解：在（1）的前提下，△ABC满足∠ACB=90°时，四边形AECF是正方形；理由如下：
∵由（2）得：当点O运动到AC的中点时，四边形AECF是矩形，
∵MN∥BC，当∠ACB=90°时，
∴∠AOE=∠ACB=90°，
∴AC⊥EF，
∴四边形AECF是菱形，
∴四边形AECF是正方形．

点评 本题考查了平行线的性质、等腰三角形的判定、矩形的判定、菱形的判定、正方形的判定；熟练掌握平行线的性质和矩形、菱形的判定方法，证明四边形AECF是菱形是解决（2）的关键．