��Ŀ����
8����ƽ��ֱ������ϵxOy�У���A��x1��y1����B��x2��y2������x1x2+y1y2=0����A��B����Ϊԭ�㣬���A��B��Ϊ�����㣮���磺A��1��1����B��2��-2��������1��2+1����-2��=0����ôA��B��Ϊ�����㣮��1����P��Q��Ϊ�����㣬P������Ϊ��-2��3����
�����Q������Ϊ��6��m������ôm��ֵΪ4��
�����Q������Ϊ��x��y������y��x֮��Ĺ�ϵʽ��
��2����M��N��Ϊ�����㣬ֱ��д����MON�Ķ�����
��3����C��D���ԣ�0��2��ΪԲ�ģ��뾶Ϊ2��Բ�ϵ������㣬���߶�CDΪ�ߣ�����������CDEF��ԭ��O��������CDEF���ⲿ�����߶�OE���ȵ�ȡֵ��Χ��
���� ��1���٢ڸ��ݻ�Ϊ������Ķ��壬�г����̼��ɽ�����⣻
��2����M��m��n����N��p��q�����Ƴ�ֱ��OM�Ľ���ʽΪy=$\frac{n}{m}$x��ֱ��ON�Ľ���ʽΪy=$\frac{q}{p}$x���ɵ�M��N��Ϊ�����㣬�ɵ�mp+nq=0���Ƴ�kOM•kON=$\frac{nq}{mp}$=-1���ɽ�����⣻
��3����ͼ1�У�����EF��CD��H����FQ��CD��Q��Ѱ������λ�ã����OE�����ֵ�Լ���Сֵ���ɣ�
��� �⣺��1���������⣺-2��6+3m=0��
���m=4��
�ʴ�Ϊ4��
�������⣺-2x+3y=0��
��y=$\frac{2}{3}$x��
�ʴ�Ϊy=$\frac{2}{3}$x��
��2����M��m��n����N��p��q����
��ֱ��OM�Ľ���ʽΪy=$\frac{n}{m}$x��ֱ��ON�Ľ���ʽΪy=$\frac{q}{p}$x��
�ߵ�M��N��Ϊ�����㣬
��mp+nq=0��
��kOM•kON=$\frac{nq}{mp}$=-1��
��OM��ON��
���MON=90�㣮
��3����ͼ1�У�����EF��CD��H����FQ��CD��Q��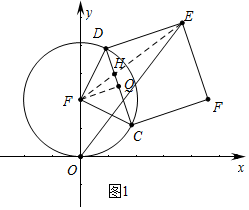
������DF=CF=2��CD=DE=2$\sqrt{2}$��DQ=QC=FQ=$\sqrt{2}$��
��FQ��DE��
��QH��DH=FQ��DE=FH��EH=1��2��
��HQ=$\frac{\sqrt{2}}{3}$��FH=$\sqrt{��\sqrt{2}��^{2}+��\frac{\sqrt{2}}{3}��^{2}}$=$\frac{2\sqrt{5}}{3}$��
��EH=2FH=$\frac{4\sqrt{5}}{3}$��
��EF=FH+EH=2$\sqrt{5}$��
�ڡ�OFE�У�OE��EF+OF��
�൱��E��y�����������ʱ��O��F��E���ߣ���ʱOE��ֵ������ֵΪ2+2$\sqrt{5}$��
��ԭ��O��������CDEF���ⲿ��
�൱��F��x����������ʱ��OE��ֵ��С����СֵΪ4��
�����������OE�ķ�ΧΪ��4��OE��2+2$\sqrt{5}$��
���� ���⿼���ı����ۺ��⡢�����ε����ʡ�һ�κ�����Ӧ�á���ֱ�ߴ�ֱ���ж���֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ��Ѱ�����������ֵ���⣬�����п�ѹ���⣮

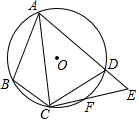 ��ͼ���ı���ABCD�ڽ��ڡ�O��F��$\widehat{CD}$��һ�㣬��$\widehat{DF}$=$\widehat{BC}$������CF���ӳ���AD���ӳ����ڵ�E������AC������ABC=105�㣬��BAC=30�㣬���E�Ķ���Ϊ��������
��ͼ���ı���ABCD�ڽ��ڡ�O��F��$\widehat{CD}$��һ�㣬��$\widehat{DF}$=$\widehat{BC}$������CF���ӳ���AD���ӳ����ڵ�E������AC������ABC=105�㣬��BAC=30�㣬���E�Ķ���Ϊ��������| A�� | 45�� | B�� | 50�� | C�� | 55�� | D�� | 60�� |
| A�� | 3$\sqrt{2}$+4$\sqrt{3}$=7$\sqrt{5}$ | B�� | 5$\sqrt{2}$-3$\sqrt{2}$=2$\sqrt{2}$ | C�� | $\sqrt{2}$��$\sqrt{3}$=$\sqrt{5}$ | D�� | 6$\sqrt{5}$��2$\sqrt{5}$=3$\sqrt{5}$ |
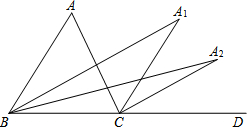 ��ͼ����ACD�ǡ�ABC����ǣ���1�β�������ABC��ƽ�������ACD��ƽ���߽��ڵ�A1����2�β�������A1BC��ƽ�������A1CD��ƽ���߽��ڵ�A2������n�β�������An-1BC��ƽ�������An-1CD��ƽ���߽��ڵ�An�����A2���A֮���������ϵ�ǡ�A2=$\frac{1}{4}$��A������A=64�㣬��An��4�㣬��n��ȡֵ��Χ��n��4��
��ͼ����ACD�ǡ�ABC����ǣ���1�β�������ABC��ƽ�������ACD��ƽ���߽��ڵ�A1����2�β�������A1BC��ƽ�������A1CD��ƽ���߽��ڵ�A2������n�β�������An-1BC��ƽ�������An-1CD��ƽ���߽��ڵ�An�����A2���A֮���������ϵ�ǡ�A2=$\frac{1}{4}$��A������A=64�㣬��An��4�㣬��n��ȡֵ��Χ��n��4�� ��ͼ��A��E��F��C��һ��ֱ���ϣ�AF=CE����E��F�ֱ���DE��AC��BF��AC������ֱ�ΪE��F��AB=CD����֤��BF=DE��
��ͼ��A��E��F��C��һ��ֱ���ϣ�AF=CE����E��F�ֱ���DE��AC��BF��AC������ֱ�ΪE��F��AB=CD����֤��BF=DE��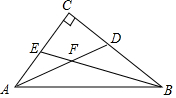 ��֪����ͼ��ʾ��Rt��ABC�У���C=90�㣬��A����B��ƽ����AD��BE����F�����AFB�Ķ�����
��֪����ͼ��ʾ��Rt��ABC�У���C=90�㣬��A����B��ƽ����AD��BE����F�����AFB�Ķ����� ��ͼ��AB�ǰ�ԲO��ֱ������C�ڰ�ԲO�ϣ�AB=4cm����CAB=60�㣬P�ǻ�$\widehat{BC}$�ϵ�һ�����㣬����AP����C����CD��AP��D������BD���ڵ�P�ƶ��Ĺ����У�BD����Сֵ�ǣ�$\sqrt{13}$-1��cm��
��ͼ��AB�ǰ�ԲO��ֱ������C�ڰ�ԲO�ϣ�AB=4cm����CAB=60�㣬P�ǻ�$\widehat{BC}$�ϵ�һ�����㣬����AP����C����CD��AP��D������BD���ڵ�P�ƶ��Ĺ����У�BD����Сֵ�ǣ�$\sqrt{13}$-1��cm��