题目内容
15.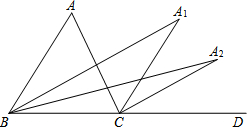 如图,∠ACD是△ABC的外角,第1次操作:∠ABC的平分线与∠ACD的平分线交于点A1;第2次操作:∠A1BC的平分线与∠A1CD的平分线交于点A2,…第n次操作:∠An-1BC的平分线与∠An-1CD的平分线交于点An,则∠A2与∠A之间的数量关系是∠A2=$\frac{1}{4}$∠A;若∠A=64°,∠An≤4°,则n的取值范围是n≥4.
如图,∠ACD是△ABC的外角,第1次操作:∠ABC的平分线与∠ACD的平分线交于点A1;第2次操作:∠A1BC的平分线与∠A1CD的平分线交于点A2,…第n次操作:∠An-1BC的平分线与∠An-1CD的平分线交于点An,则∠A2与∠A之间的数量关系是∠A2=$\frac{1}{4}$∠A;若∠A=64°,∠An≤4°,则n的取值范围是n≥4.
分析 (1)根据角平分线的定义可得∠A1BC=$\frac{1}{2}$∠ABC,∠A1CD=$\frac{1}{2}$∠ACD,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,整理即可求出∠A1的度数,同理求出∠A2;
(2)根据计算结果,发现后一个角等于前一个角的$\frac{1}{2}$的规律即可得∠An=$\frac{1}{{2}^{n}}$∠A,再把∠A=64°代入∠An=$\frac{1}{{2}^{n}}$∠A≤4°解答即可.
解答 解:∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=$\frac{1}{2}$∠ABC,∠A1CD=$\frac{1}{2}$∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴$\frac{1}{2}$(∠A+∠ABC)=$\frac{1}{2}$∠ABC+∠A1,
∴∠A1=$\frac{1}{2}$∠A,
同理可得∠A2=$\frac{1}{2}$∠A1=$\frac{1}{4}$∠A;
根据以上规律可得∠An=$\frac{1}{{2}^{n}}$∠A,
当∠A=64°,∠An≤4°时,$\frac{1}{{2}^{n}}$∠A≤4°,
解得n≥4,
故答案为:∠A2=$\frac{1}{4}$∠A,n≥4.
点评 本题考查的是三角形内角和定理,根据角平分线的定义可得∠A1BC=$\frac{1}{2}$∠ABC,∠A1CD=$\frac{1}{2}$∠ACD是解答此题的关键.

练习册系列答案
相关题目
4.若81-xn=(3-x)(3+x)(9+x2),则n的值为( )
| A. | 2 | B. | 3 | C. | 6 | D. | 4 |
 如图,在平面直角坐标系xOy中,抛物线y=$\frac{1}{4}$x2+bx+c经过点A(-2,0)和原点,点B在抛物线上且tan∠BAO=$\frac{1}{2}$,抛物线的对称轴与x轴相交于点P.
如图,在平面直角坐标系xOy中,抛物线y=$\frac{1}{4}$x2+bx+c经过点A(-2,0)和原点,点B在抛物线上且tan∠BAO=$\frac{1}{2}$,抛物线的对称轴与x轴相交于点P. 如图:证明:∠A+∠B+∠C=180°.
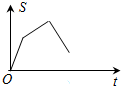
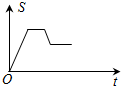
如图:证明:∠A+∠B+∠C=180°.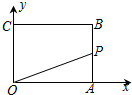 如图,已知矩形OABC,A(6,0),C(0,4),动点P从点A出发,沿A-B-C的路线以每秒2个单位长度的速度运动,设线段OP在运动过程中扫过矩形的面积为S,则下列能大致反映面积S与运动时间t(秒)之间关系的图象是( )
如图,已知矩形OABC,A(6,0),C(0,4),动点P从点A出发,沿A-B-C的路线以每秒2个单位长度的速度运动,设线段OP在运动过程中扫过矩形的面积为S,则下列能大致反映面积S与运动时间t(秒)之间关系的图象是( )