题目内容
13. 如图,AB是半圆O的直径,点C在半圆O上,AB=4cm,∠CAB=60°,P是弧$\widehat{BC}$上的一个动点,连接AP,过C点作CD⊥AP于D,连接BD,在点P移动的过程中,BD的最小值是($\sqrt{13}$-1)cm.
如图,AB是半圆O的直径,点C在半圆O上,AB=4cm,∠CAB=60°,P是弧$\widehat{BC}$上的一个动点,连接AP,过C点作CD⊥AP于D,连接BD,在点P移动的过程中,BD的最小值是($\sqrt{13}$-1)cm.
分析 以AC为直径作圆O′,连接BO′、BC.在点P移动的过程中,点D在以AC为直径的圆上运动,当O′、D、B共线时,BD的值最小,最小值为O′B-O′D,利用勾股定理求出BO′即可解决问题.
解答 解:如图,以AC为直径作圆O′,连接BO′、BC.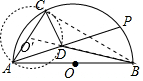
∵CD⊥AP,
∴∠ADC=90°,
∴在点P移动的过程中,点D在以AC为直径的圆上运动,
∵AB是直径,
∴∠ACB=90°,
在Rt△ABC中,∵AB=4cm,∠CAB=60°,
∴BC=AB•sin60°=2$\sqrt{3}$,AC=AB•cos60°=2cm.
在Rt△BCO′中,BO′=$\sqrt{B{C}^{2}+O′{C}^{2}}$=$\sqrt{12+1}$=$\sqrt{13}$,
∵O′D+BD≥O′B,
∴当O′、D、B共线时,BD的值最小,最小值为O′B-O′D=$\sqrt{13}$-1,
故答案为($\sqrt{13}$-1)cm.
点评 本题考查圆周角定理,勾股定理、点与圆的位置关系等知识,解题的关键是确定点D的运动轨迹是以AC为直径的圆上运动,属于中考填空题中的压轴题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
19.如果函数y=(a-1)x2+3x+a+5的图象经过平面直角坐标系的三个象限,那么a的取值范围是( )
| A. | a≥-5 | B. | a<1 | ||
| C. | -1<a<-2+$\frac{3\sqrt{5}}{2}$ | D. | -2-$\frac{3\sqrt{5}}{2}$<a<-5或1<a<-2+$\frac{3\sqrt{5}}{2}$ |
4.若81-xn=(3-x)(3+x)(9+x2),则n的值为( )
| A. | 2 | B. | 3 | C. | 6 | D. | 4 |
5.点A在第二象限,且到x轴的距离为2,到y轴的距离为3,则点A的坐标是( )
| A. | (-2,3) | B. | (-3,2) | C. | (3,-2) | D. | (2,-3) |
2. 如图,在Rt△ABC中,∠ACB=90°,AC=BC,点M在AC边上,且AM=1,MC=4,动点P在AB边上,连接PC,PM,则PC+PM的最小值是( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC,点M在AC边上,且AM=1,MC=4,动点P在AB边上,连接PC,PM,则PC+PM的最小值是( )
 如图,在Rt△ABC中,∠ACB=90°,AC=BC,点M在AC边上,且AM=1,MC=4,动点P在AB边上,连接PC,PM,则PC+PM的最小值是( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC,点M在AC边上,且AM=1,MC=4,动点P在AB边上,连接PC,PM,则PC+PM的最小值是( )| A. | $\sqrt{17}$ | B. | 6 | C. | $\sqrt{26}$ | D. | 7 |
3.不等式组$\left\{\begin{array}{l}{2x+3≥x+11}\\{\frac{2x+5}{3}>2-x}\end{array}\right.$的解集是( )
| A. | x>$\frac{4}{5}$ | B. | x≥8 | C. | $\frac{4}{5}$<x≤8 | D. | 无解 |
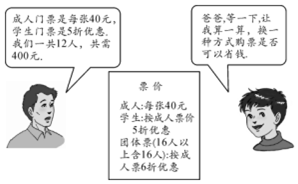 在“五一”期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
在“五一”期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题: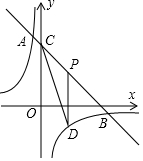 如图,直线y=-x+8与双曲线y=$\frac{k}{x}$相交于A,B两点,与y轴交于点C,点P是线段BC上的动点(点P不与点B,C重合),过P作y轴的平行线,交双曲线于点D,连接CD,若点A的横坐标为-1,则△PDC的面积的最大值为$\frac{25}{2}$.
如图,直线y=-x+8与双曲线y=$\frac{k}{x}$相交于A,B两点,与y轴交于点C,点P是线段BC上的动点(点P不与点B,C重合),过P作y轴的平行线,交双曲线于点D,连接CD,若点A的横坐标为-1,则△PDC的面积的最大值为$\frac{25}{2}$.