题目内容
3．
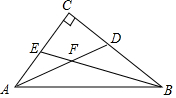已知：如图所示，Rt△ABC中，∠C=90°，∠A、∠B的平分线AD、BE交于F，求∠AFB的度数．
分析 先根据∠C=90°，求得∠CAB+∠CBA=90°，再根据AD、BE平分∠CAB、∠CBA，即可得到∠FAB+∠FBA=45°，最后根据三角形内角和定理即可得到∠AFB=135°．
解答 解：∵∠C=90°，
∴∠CAB+∠CBA=90°，
∵AD、BE平分∠CAB、∠CBA，
∴∠FAB+∠FBA=45°，
∴∠AFB=135°．
点评 本题主要考查了直角三角形的性质以及三角形内角和定理的运用，解题时注意：有一个角为90°的三角形，叫做直角三角形．
练习册系列答案
相关题目
如图，在正方形ABCD中，△APBC是等边三角形，连接PD，DB，则$\frac{{S}_{△BPD}}{{S}_{正方形ABCD}}$=$\frac{\sqrt{3}-1}{4}$．
如图，在平面直角坐标系xOy中，抛物线y=$\frac{1}{4}$x2+bx+c经过点A（-2，0）和原点，点B在抛物线上且tan∠BAO=$\frac{1}{2}$，抛物线的对称轴与x轴相交于点P．
如图：证明：∠A+∠B+∠C=180°．
18．
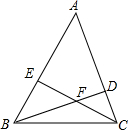如图，△ABC的两条高线BD，CE相交于点F，已知∠ABC=60°，AB=10，CF=EF，则△ABC的面积为（ ）
如图，△ABC的两条高线BD，CE相交于点F，已知∠ABC=60°，AB=10，CF=EF，则△ABC的面积为（ ）| A． | 20$\sqrt{3}$ | B． | 25$\sqrt{3}$ | C． | 30$\sqrt{3}$ | D． | 40$\sqrt{3}$ |
如图，在△ABC中，AC=BC，∠ACB=90°，点D在BC的延长线上，连接AD，过B作BE⊥AD，垂足为E，交AC于点F，连接CE．
13．在方程2x+3y=5中，用含y的代数式表示x正确的是（ ）
| A． | y=$\frac{5-2x}{3}$ | B． | y=$\frac{2x-5}{3}$ | C． | x=$\frac{5-3y}{2}$ | D． | x=$\frac{3y-5}{2}$ |