Question

7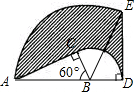．如图，△ABC中，∠C是直角，AB=6cm，∠ABC=60°，将△ABC以点B为中心顺时针旋转，使点C旋转到AB边延长线上的D处，则AC边扫过的图形众人阴影部分的面积是9π．

Answer 1

分析 由将△ABC以点B为中心顺时针旋转，使点C旋转到AB的延长线上的点D处，可得△ABC≌△EBD，由题给图象可知：S_阴影=S_扇形ABE+S_△BDE-S_△ABC-S_扇形BCD=S_扇形ABE-S_扇形BCD可得出阴影部分面积．

解答 解：∵△ABC中，∠C是直角，AB=6cm，∠ABC=60°
∴AC=3$\sqrt{3}$cm，BC=3cm．
∵将△ABC以点B为中心顺时针旋转，使点C旋转到AB的延长线上的点D处，
∴△ABC≌△EBD．
由题给图象可知：
S_阴影=S_扇形ABE+S_△BDE-S_△ABC-S_扇形BCD
=$\frac{120π•{6}^{2}}{360}$+$\frac{1}{2}$×3×3$\sqrt{3}$-$\frac{1}{2}$×3×3$\sqrt{3}$-$\frac{120π×{3}^{2}}{360}$
=12π-3π
=9π．
故答案为：9π．

点评 本题考查的是扇形面积的计算，熟记扇形的面积公式是解答此题的关键．