题目内容
8. 符合数轴所表示的解集的不等式组是( )
符合数轴所表示的解集的不等式组是( )| A. | $\left\{\begin{array}{l}{x+1>0}\\{4-x>0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+1>0}\\{x-4>0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+1<0}\\{x-4>0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+1<0}\\{4-x>0}\end{array}\right.$ |
分析 先求出不等式组中每一个不等式的解集,再求出它们的公共部分,然后把不等式的解集表示在数轴上即可.
解答 解:A、的解集是-1<x<4,故A符合题意;
B、的解集是x>4,故B不符合题意;
C、无解,故C不符合题意;
D、的解集是x<-1,故D不符合题意;
故选:A.
点评 本题考查了在数轴上表示不等式的解集,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
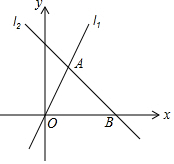 如图,在平面直角坐标系xOy中,直线l1:y=mx(m≠0)与直线l2:y=ax+b(a≠0)相交于点A(2,4),直线l2与x轴交于点B(6,0).
如图,在平面直角坐标系xOy中,直线l1:y=mx(m≠0)与直线l2:y=ax+b(a≠0)相交于点A(2,4),直线l2与x轴交于点B(6,0). 如图,点O在直线AB上,OC⊥OD,OC,OF分别平分∠AOE和∠BOD,若∠AOC=20°,则∠BOF的度数为35°.
如图,点O在直线AB上,OC⊥OD,OC,OF分别平分∠AOE和∠BOD,若∠AOC=20°,则∠BOF的度数为35°.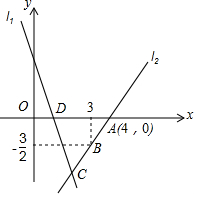 如图,直线l1的表达式为y=-3x+3,且与x轴交于点D,直线l2经过点A(4,0),B(3,-$\frac{3}{2}$),直线l1,l2交于点C.
如图,直线l1的表达式为y=-3x+3,且与x轴交于点D,直线l2经过点A(4,0),B(3,-$\frac{3}{2}$),直线l1,l2交于点C.
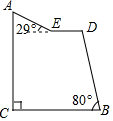 “蘑菇石”是我国著名的自然保护区梵净山的标志,小明从山脚B点先乘坐缆车到达观景平台DE观景,然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点,“蘑菇石”A点到水平面BC的垂直距离为1890m.如图,DE∥BC,BD=1800m,∠DBC=80°,求斜坡AE的长度.(结果精确到0.1m,可参考数据sin29°≈0.4848,sin80°≈0.9848,cos29°≈0.8746,cos80°≈0.1736)
“蘑菇石”是我国著名的自然保护区梵净山的标志,小明从山脚B点先乘坐缆车到达观景平台DE观景,然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点,“蘑菇石”A点到水平面BC的垂直距离为1890m.如图,DE∥BC,BD=1800m,∠DBC=80°,求斜坡AE的长度.(结果精确到0.1m,可参考数据sin29°≈0.4848,sin80°≈0.9848,cos29°≈0.8746,cos80°≈0.1736)