题目内容
7.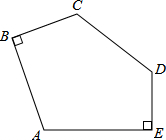 如图,已知AB=CD=AE=BC+DE=4,∠ABC=∠AED=90°,则五边形ABCDE的面积为16.
如图,已知AB=CD=AE=BC+DE=4,∠ABC=∠AED=90°,则五边形ABCDE的面积为16.
分析 延长DE到F,使EF=BC,连接AC,AD,AF,利用SAS得到三角形ABC与三角形AEF全等,利用全等三角形的对应边相等得到AC=AF,根据CD=BC+DE,EF=BC,等量代换得到CD=DF,利用SSS得到三角形ACD与三角形AFD全等,根据三角形ABC与三角形AEF全等,得到五边形ABCDE等于三角形ADF的2倍,求出即可.
解答 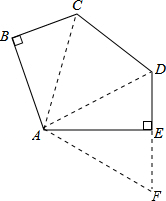 解:延长DE到F,使EF=BC,连接AC,AD,AF,
解:延长DE到F,使EF=BC,连接AC,AD,AF,
在△ABC和△AEF中,
$\left\{\begin{array}{l}{AB=AE}\\{∠B=∠AEF}\\{BC=EF}\end{array}\right.$,
∴△ABC≌△AEF(SAS),
∴AC=AF,
∵CD=BC+DE,EF=BC,
∴CD=DF,
在△ACD和△AFD中,
$\left\{\begin{array}{l}{AC=AF}\\{CD=DF}\\{AD=AD}\end{array}\right.$,
∴△ACD≌△AFD(SSS),
∵△ABC≌△AEF,
∴S△ABC=S△AEF,
∴S五边形ABCDE=S△ABC+S四边形AEDC=S△AEF+S四边形AEDC=2S△ADF,
∵AB=CD=AE=4,∠AED=90°,
∴S△ADF=8,
则S五边形ABCDE=16.
故答案为:16
点评 此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.若a是最大的负整数,b是绝对值最小的有理数,c是倒数等于它本身的自然数,则代表式a2015+2016b+c2017的值为( )
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 0 |
12.直角三角形中,一直角边的长为6,斜边的长为9,那么斜边上的高将这个直角三角形分成的两个小三角形的面积比是( )
| A. | $\sqrt{5}$:2 | B. | 4:5 | C. | 3:5 | D. | 10:25 |
19.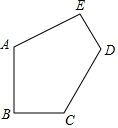 如图,已知AB=AE=$\sqrt{3}$,BC=DE=1,∠B=∠E=90°,∠A=120°,五边形ABCDE的面积是( )
如图,已知AB=AE=$\sqrt{3}$,BC=DE=1,∠B=∠E=90°,∠A=120°,五边形ABCDE的面积是( )
 如图,已知AB=AE=$\sqrt{3}$,BC=DE=1,∠B=∠E=90°,∠A=120°,五边形ABCDE的面积是( )
如图,已知AB=AE=$\sqrt{3}$,BC=DE=1,∠B=∠E=90°,∠A=120°,五边形ABCDE的面积是( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 8 | D. | 4$\sqrt{3}$ |
16. 如图,数轴上点A,B,C分别表示有理数a,b,c,若ac<0,a+b>0,则原点位于( )
如图,数轴上点A,B,C分别表示有理数a,b,c,若ac<0,a+b>0,则原点位于( )
 如图,数轴上点A,B,C分别表示有理数a,b,c,若ac<0,a+b>0,则原点位于( )
如图,数轴上点A,B,C分别表示有理数a,b,c,若ac<0,a+b>0,则原点位于( )| A. | 点A的左侧 | B. | 点A与点B之间 | C. | 点B与点C之间 | D. | 在点C的右侧 |
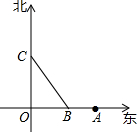 如图,甲船从点O出发,自南向北以40海里/时的速度行驶;乙船在点O正东方向120海里的A处,以30海里/时的速度自东向西行驶,经过2或$\frac{22}{25}$小时两船的距离为100海里.
如图,甲船从点O出发,自南向北以40海里/时的速度行驶;乙船在点O正东方向120海里的A处,以30海里/时的速度自东向西行驶,经过2或$\frac{22}{25}$小时两船的距离为100海里.