题目内容
8.矩形ABCD中,AB=6,BC=8,点E在BC上,将△ABE沿直线AE折叠,点B落在矩形内部的点F处,连接DF,当△ADF是等腰三角形时,cos∠DAF=$\frac{2}{3}$或$\frac{3}{8}$.分析 如图1或2,运用分类讨论的数学思想,按FA=FD或DA=DF两种情况分类解析,分别求出AG的长度,即可解决问题.
解答  解:如图1,由题意得:
解:如图1,由题意得:
AD=BC=8,AF=AB=6;
若FA=FD,过点F作FG⊥AD于点G;
则AG=BG=4,
∴cos∠DAF=$\frac{AG}{AF}=\frac{4}{6}=\frac{2}{3}$;
如图2,若DA=DF,过点D作DG⊥AF于点G;
则AG=FG=3,cos∠DAF=$\frac{AG}{AD}$=$\frac{3}{8}$,
综上所述,该题答案为$\frac{2}{3}$或$\frac{3}{8}$.
点评 该题以矩形为载体,以考查矩形的性质、翻折变换的性质、等腰三角形的性质等几何知识点为核心构造而成;解题的关键是根据题意,正确作出符合题意的图形;灵活运用矩形的性质、翻折变换的性质等几何知识点来分析、判断、解答.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
19.小馨和小霏是七(1)班的学生,两人既是好朋友,又是学习上的竞争对手.她们约定在本次的期末考试中比一比谁的总分高.(考试科目见下表,每门课的满分为100分,单科分数均为整数)下表是她们期末考试的部分成绩.
根据表格显示的数据,小霏同学数学成绩至少91 分,她的总分才有可能比小馨总分高.
| 姓名 | 语文 | 数学 | 英语 | 政治 | 历史 |
| 小馨 | 86 | 98 | 100 | 96 | 97 |
| 小霏 | 88 | 99 |
3.下列计算正确的是( )
| A. | a3+a2=a5 | B. | a3-a2=a | C. | a2•a4=a8 | D. | a3÷a2=a |
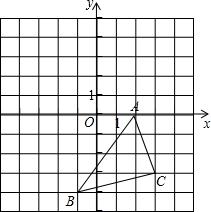 在如图所示的直角坐标系中,解答下列问题:
在如图所示的直角坐标系中,解答下列问题: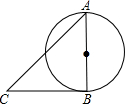 如图,AB是⊙O直径,BC是⊙O的切线,AB=BC,求∠A的度数.
如图,AB是⊙O直径,BC是⊙O的切线,AB=BC,求∠A的度数.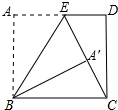 如图,矩形ABCD中,AB=15cm,点E在AD上,AE=9cm,连接EC,将矩形ABCD沿BE翻折,点A恰好落在EC上的点A′处,则BC=17cm.
如图,矩形ABCD中,AB=15cm,点E在AD上,AE=9cm,连接EC,将矩形ABCD沿BE翻折,点A恰好落在EC上的点A′处,则BC=17cm.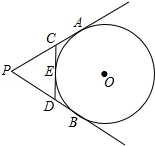 如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为r,△PCD的周长等于3r,则sin∠APB的值是$\frac{12}{13}$.
如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为r,△PCD的周长等于3r,则sin∠APB的值是$\frac{12}{13}$.