题目内容
18.已知点A(a-2b,2-4ab)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴的对称点坐标为(0,10).分析 先根据二次函数图象上点的坐标特征,把A(a-2b,2-4ab)代入y=x2+4x+10后整理得(a+2)2+4(b-1)2=0,根据非负数的性质解得a=-2,b=1,则点A的坐标为(-4,10),再计算出抛物线的对称轴方程,然后利用对称的性质求解.
解答 解:把A(a-2b,2-4ab)代入y=x2+4x+10得
(a-2b)2+4(a-2b)+10=2-4ab,
整理得a2+4a+4b2-8b+8=0,
(a+2)2+4(b-1)2=0,解得a=-2,b=1,
则点A的坐标为(-4,10),
因为抛物线的对称轴为直线x=-$\frac{4}{2}$=-2,
所以点A(-4,10)关于直线x=-2的对称点的坐标为(0,10).
故答案为(0,10).
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.化简:(m+1)2-(1-m)(1+m)正确的结果是( )
| A. | 2m2 | B. | 2m+2 | C. | 2m2+2m | D. | 0 |
6.下列计算正确的是( )
| A. | 3ab-2ab=1 | B. | ($\sqrt{2}$+1)(1-$\sqrt{2}$)=1 | C. | -(-a)4÷a2=a2 | D. | $\root{3}{-8}$=-2 |
13.已知边长为a的正方形面积为10,则下列关于a的说法中:
①a是无理数;②a是方程x2-10=0的解;③a是10的算术平方根; ④a满足不等式组$\left\{\begin{array}{l}{a-3>0}\\{a-4<0}\end{array}\right.$
正确的说法有( )
①a是无理数;②a是方程x2-10=0的解;③a是10的算术平方根; ④a满足不等式组$\left\{\begin{array}{l}{a-3>0}\\{a-4<0}\end{array}\right.$
正确的说法有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
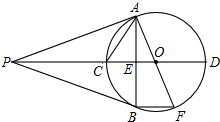 如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于C、D,交AB于E,AF为⊙O的直径,有下列结论:
如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于C、D,交AB于E,AF为⊙O的直径,有下列结论: 如图,在直线a、b、c、d构成的角中,已知∠1=∠3,∠2=110°,求∠4的度数.
如图,在直线a、b、c、d构成的角中,已知∠1=∠3,∠2=110°,求∠4的度数.