题目内容
18.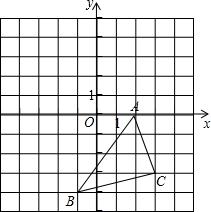 在如图所示的直角坐标系中,解答下列问题:
在如图所示的直角坐标系中,解答下列问题:(1)将△ABC绕点A顺时针旋转90°,画出旋转后的△AB1C1;
(2)直接写出B1,C1的坐标;
(3)直接写出△ABC在运动过程中扫过的面积.(结果保留π).
分析 (1)据题意所述,旋转中心为点A,旋转角度为90°,旋转方向为顺时针可找出各点的对称点,从而顺次连接可得出△AB1C1;
(2)根据图形即可写出B1,C1的坐标;
(3)△ABC扫过的面积是扇形BAB1的面积与△ABC面积的和.
解答 解:(1)所画图形如下:
(2)如图,B1的坐标为(-2,3),C1的坐标(-1,-1);
(3)∵将△ABC绕点A顺时针旋转90°到△AB1C1的位置,
∴∠BAB1=90°,
∵AB=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴扇形BAB1的面积=$\frac{90π×{5}^{2}}{360}$=$\frac{25π}{4}$,
∵△ABC的面积=4×4-$\frac{1}{2}$×4×3-$\frac{1}{2}$×4×1-$\frac{1}{2}$×3×1=16-6-2-$\frac{3}{2}$=$\frac{13}{2}$,
∴△ABC扫过的面积=扇形BAB1的面积+△ABC面积=$\frac{25π}{4}$+$\frac{13}{2}$=$\frac{25π+26}{4}$.
点评 此题考查了作图-旋转变换及扇形面积的计算,解答本题需要正确地作出△AB1C1,第三问比较抽象,需要我们明确△ABC在运动过程中扫过的是那一部分的面积,难度较大.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
8.下列语句中,是命题的是( )
| A. | 过直线l外一点作l的平行线 | B. | 美丽的天空 | ||
| C. | 你的作业做完了吗? | D. | 对顶角相等 |
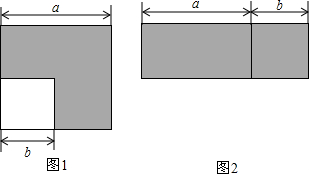 如图1,在边长为a的大正方形中有一个边长为b的小正方形,如图2是由图1中阴影部分拼成的一个长方形.
如图1,在边长为a的大正方形中有一个边长为b的小正方形,如图2是由图1中阴影部分拼成的一个长方形.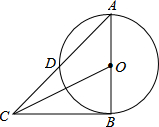 如图,在⊙O中,AB为直径,AD为弦,过点B的切线与AD的延长线交于点C.已知∠C=40°,则∠DBA的度数是40°.
如图,在⊙O中,AB为直径,AD为弦,过点B的切线与AD的延长线交于点C.已知∠C=40°,则∠DBA的度数是40°.