题目内容
13．
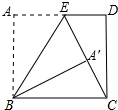如图，矩形ABCD中，AB=15cm，点E在AD上，AE=9cm，连接EC，将矩形ABCD沿BE翻折，点A恰好落在EC上的点A′处，则BC=17cm．
分析 如图，首先证明∠CEB=∠EBC，得到BC=EC=λ，此为解决该题的关键性结论；在直角△CDE中，运用勾股定理列出关于λ的方程，求出λ即可解决问题．
解答 解：如图，∵四边形ABCD为矩形，
∴DC=AB=15，AD=BC（设为λ），
∠D=90°，AD∥BC；
∴∠AEB=∠EBC；由题意得：∠AEB=∠A′EB，
∴∠CEB=∠EBC，
∴BC=EC=λ；而DE=λ-9，由勾股定理得：λ2=152+（λ-9）2，
解得：λ=17（cm）．
故答案为17．
点评 该题主要考查了矩形的性质、等腰三角形的判定、翻折变换的性质、勾股定理等几何知识点及其应用问题；应牢固掌握矩形的性质、等腰三角形的判定、翻折变换的性质等知识点，这是灵活运用、解题的基础．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
在A、B、C、D四幅图案中，哪一幅可以通过平移（1）得到（ ）
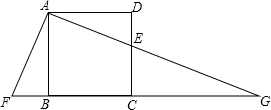如图，E是正方形ABCD的边DC上的一点，过点A作AF⊥AE，交CB延长线于点F，AE的延长线交BC的延长线于点G．若AF=7，DE=2，则EG的长是$\frac{21\sqrt{5}}{2}$-7．
如图，将一块三角板的直角顶点C放在直线EF上，使得AB∥EF，已知$cosA=\frac{1}{2}$，则sinα=$\frac{1}{2}$．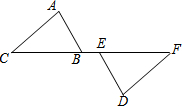
如图，点C、B、E、F在同一直线上，CE=BF，AC∥DF，AC=DF．求证：△ABC≌△DEF．
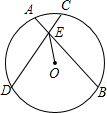如图，⊙O的两条弦AB、CD交于点E，OE平分∠BED．