题目内容
19.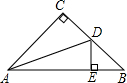 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB交AB于点E,AB=4$\sqrt{2}$cm,求△BDE的周长.
如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB交AB于点E,AB=4$\sqrt{2}$cm,求△BDE的周长.
分析 本题易证Rt△ADC≌Rt△ADE,得到AC=AE=BC,DE=CD,则△BDE的周长=DE+DB+EB=BC+EB=AE+EB=AB.
解答 解:根据题意能求出△BDE的周长.
∵∠C=90°,∠DEA=90°,
又∵AD平分∠CAB,
∴DE=DC.
在Rt△ADC和Rt△ADE中,$\left\{\begin{array}{l}{DE=DC}\\{AD=AD}\end{array}\right.$,
∴Rt△ADC≌Rt△ADE(HL).
∴AC=AE,
又∵AC=BC,
∴AE=BC.
∴△BDE的周长=DE+DB+EB=BC+EB=AE+EB=AB.
∵AB=4$\sqrt{2}$cm,
∴△BDE的周长=4$\sqrt{2}$cm.
点评 本题主要考查了全等三角形的性质,对应边相等,正确证明Rt△ADC≌Rt△ADE是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.在Rt△ABC中,∠C=90°,AB=15,AC:BC=3:4,则这个直角三角形的面积是( )
| A. | 24 | B. | 48 | C. | 54 | D. | 108 |
9.下列不等式组中,解集是2<x<3的不等式组是( )
| A. | $\left\{\begin{array}{l}x>3\\ x>2\end{array}\right.$ | B. | $\left\{\begin{array}{l}x>3\\ x<2\end{array}\right.$ | C. | $\left\{\begin{array}{l}x<3\\ x>2\end{array}\right.$ | D. | $\left\{\begin{array}{l}x<3\\ x<2\end{array}\right.$ |
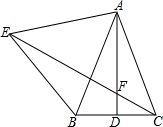 如图,△ABC中,AB=AC,AD是BC边上的中线,以AB为边向外作等边△ABE,与直线AD交于点F.
如图,△ABC中,AB=AC,AD是BC边上的中线,以AB为边向外作等边△ABE,与直线AD交于点F. 二次函数y=$\frac{2}{3}$x2的函数图象如图,点A0位于坐标原点,点A1,A2,A3…A10 在y轴的正半轴上,点B1,B2,B3…B10在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上,△A0B1A1,△A1B2A2,△A2B3A3…△A9B10A10都为等边三角形,则△A9B10A10的边长为10.
二次函数y=$\frac{2}{3}$x2的函数图象如图,点A0位于坐标原点,点A1,A2,A3…A10 在y轴的正半轴上,点B1,B2,B3…B10在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上,△A0B1A1,△A1B2A2,△A2B3A3…△A9B10A10都为等边三角形,则△A9B10A10的边长为10.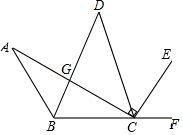 如图,AB∥CD,BD平分∠ABC,∠ACE=90°,AC⊥BD
如图,AB∥CD,BD平分∠ABC,∠ACE=90°,AC⊥BD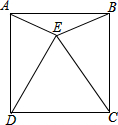 如图,E为正方形ABCD内的一点,且△DCE为等边三角形,则∠CBE=75°,∠ABE=15°.
如图,E为正方形ABCD内的一点,且△DCE为等边三角形,则∠CBE=75°,∠ABE=15°.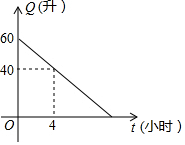 汽车油箱中的余油量Q(升)是它行驶的时间t(小时)的一次函数,某天该汽车外出时,油箱中余油量与行驶时间的变化关系如图所示,当油箱中余油20升时,该汽车行驶了8小时.
汽车油箱中的余油量Q(升)是它行驶的时间t(小时)的一次函数,某天该汽车外出时,油箱中余油量与行驶时间的变化关系如图所示,当油箱中余油20升时,该汽车行驶了8小时.