题目内容
7. 如图,⊙O的弦AB=8,P是劣弧AB中点,连结OP交AB于C,且PC=2,则⊙O的半径为( )
如图,⊙O的弦AB=8,P是劣弧AB中点,连结OP交AB于C,且PC=2,则⊙O的半径为( )| A. | 8 | B. | 4 | C. | 5 | D. | 10 |
分析 首先连接OA,由P是劣弧AB中点,可得OP⊥AB,且AC=4,然后设⊙0的半径为x,利用勾股定理即可求得方程:x2=42+(x-2)2,解此方程即可求得答案.
解答 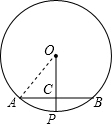 解:连接OA,
解:连接OA,
∵P是劣弧AB中点,
∴OP⊥AB,AC=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4,
设⊙0的半径为x,则OC=OP-PC=x-2,
在Rt△OAC中,OA2=OC2+AC2,
∴x2=42+(x-2)2,
解得:x=5,
∴⊙0的半径为5.
故选C.
点评 此题考查了垂径定理以及勾股定理.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
18.下列代数式:①$\frac{2}{x}$,②$\frac{x+y}{5}$,③$\frac{1}{2-a}$,$\frac{x}{3}+\frac{3}{x}$.其中是分式的有( )
| A. | ①②③ | B. | ①②③④ | C. | ①③④ | D. | ①②④ |
 有一道作业题:解方程$\frac{2x-1}{3}$=1-$\frac{x+2}{4}$.下面的纸片上是小明的解答过程:
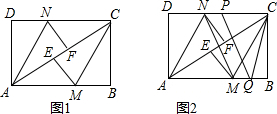
有一道作业题:解方程$\frac{2x-1}{3}$=1-$\frac{x+2}{4}$.下面的纸片上是小明的解答过程: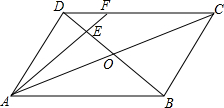 如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,若DF=2,则FC=4.
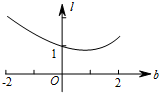
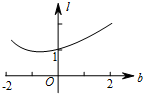
如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,若DF=2,则FC=4.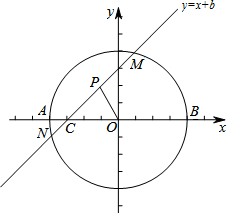 如图在直角坐标系中,已知A(-2,0),B(2,0).直线y=x+b(-2≤b≤2)交x轴于点C,交以AB为直径的⊙O于M,N两点(M在N的上方),点P是MC的中点(当M,C点重合时,点P即是点M).设线段OP的长度为l,则下列图象中大致能表示l与b之间的函数关系的图象是( )
如图在直角坐标系中,已知A(-2,0),B(2,0).直线y=x+b(-2≤b≤2)交x轴于点C,交以AB为直径的⊙O于M,N两点(M在N的上方),点P是MC的中点(当M,C点重合时,点P即是点M).设线段OP的长度为l,则下列图象中大致能表示l与b之间的函数关系的图象是( )