题目内容
8.当1<x<3时,$\sqrt{{{({1-x})}^2}}+\sqrt{{x^2}-6x+9}$=2.分析 因为1-x<0,x-3>0,由二次根式的性质得到$\sqrt{(1-x)^{2}}$=x-1,$\sqrt{(x-3)^{2}}$=3-x,最后求得结果.
解答 解:$\sqrt{(1-x)^{2}}+\sqrt{{x}^{2}-6x+9}$
=$\sqrt{(1-x)^{2}}+\sqrt{(x-3)^{2}}$
=x-1+3-x
=2.
故答案为2.
点评 本题主要考查了二次根式的性质:$\sqrt{{a}^{2}}$=$\left\{\begin{array}{l}{a(a≥0)}\\{-a(a<0)}\end{array}\right.$,灵活应用性质是解题的关键.

练习册系列答案
相关题目
13.下列方程中是二元一次方程的是( )
| A. | 3x-2y=4z | B. | 6xy+13=0 | C. | 3x=y-1 | D. | $\frac{1}{x}$+3y=2 |
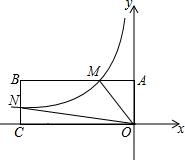 如图,在平面直角坐标系中,矩形OABC的顶点O与坐标原点重合,OC在x轴的负半轴上,OA在y轴的正半轴上,顶点B的坐标为(-6,1).反比例函数y=-$\frac{2}{x}$(x<0)的图象与AB交于点M,与BC交于点N,若点P在y轴上,使S△OMP=S四边形OMBN,则点P的坐标为(0,4)或(0,-4).
如图,在平面直角坐标系中,矩形OABC的顶点O与坐标原点重合,OC在x轴的负半轴上,OA在y轴的正半轴上,顶点B的坐标为(-6,1).反比例函数y=-$\frac{2}{x}$(x<0)的图象与AB交于点M,与BC交于点N,若点P在y轴上,使S△OMP=S四边形OMBN,则点P的坐标为(0,4)或(0,-4).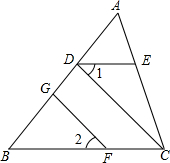 如图,已知:∠ADE=∠B,∠2=∠1,GF⊥AB,则CD⊥AB吗?请说明理由.
如图,已知:∠ADE=∠B,∠2=∠1,GF⊥AB,则CD⊥AB吗?请说明理由.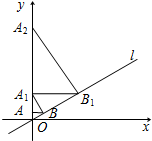 如图,已知直线l:y=$\frac{\sqrt{3}}{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点A5的坐标为(0,210).
如图,已知直线l:y=$\frac{\sqrt{3}}{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点A5的坐标为(0,210).