题目内容
如图,在四边形ABCD中,∠BAD=∠B=∠C=90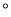 ,AD=BC=20,AB=DC=16.将四边形ABCD沿直线AE折叠,使点D落在BC边上的点F处.
,AD=BC=20,AB=DC=16.将四边形ABCD沿直线AE折叠,使点D落在BC边上的点F处.
(1)求BF的长;
(2)求CE的长.
(1);(2) 【解析】试题分析:由折叠的性质可得:AF=AD=20,再由勾股定理可求出BF=12. (2)设CE=x,DE=EF=16-x,然后利用勾股定理得到,再解方程求出x即可. (1)∵△AFE是△ADE折叠得到的, ∴. 在Rt△ABE中, (2)∵△AFE是△ADE折叠得到的, ∴. 设,则 在Rt△EFC中, 即 解得...
练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目


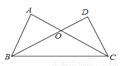
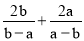 ;(3)
;(3) 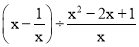 .
.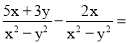 _______.
_______.
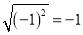 B. 22×23=26 C. 20=0 D. (﹣1)﹣2=1
B. 22×23=26 C. 20=0 D. (﹣1)﹣2=1