题目内容
已知x1,x2是关于x的一元二次方程x2﹣6x+k=0的两个实数根,且x12x22﹣x1﹣x2=115.
(1)求k的值;
(2)求x12+x22+8的值.
(1)k的值为﹣11;(2)x12+x22+8=66. 【解析】试题分析:(1)方程有两个实数根,必须满足△=b2-4ac≥0,从而求出实数k的取值范围,再利用根与系数的关系,x12x22-x1-x2=115.即x12x22-(x1+x2)=115,即可得到关于k的方程,求出k的值. (2)根据(1)即可求得x1+x2与x1x2的值,而x12+x22+8=(x1+x2)2-2x1x2+...
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


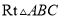 中,
中, 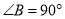 ,
, 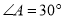 ,
, 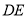 垂直平分斜边
垂直平分斜边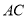 ,交
,交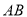 于
于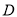 ,
, 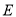 是垂足,连接
是垂足,连接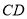 ,若
,若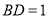 ,则
,则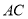 的长是__________.
的长是__________.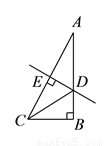


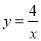 (x>0)的图象相交于A、B,设点A的坐标为(m,n),那么以m为长,n为宽的矩形的面积和周长分别为_____,_____.
(x>0)的图象相交于A、B,设点A的坐标为(m,n),那么以m为长,n为宽的矩形的面积和周长分别为_____,_____.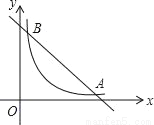
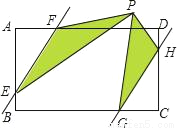
 ,AD=BC=20,AB=DC=16.将四边形ABCD沿直线AE折叠,使点D落在BC边上的点F处.
,AD=BC=20,AB=DC=16.将四边形ABCD沿直线AE折叠,使点D落在BC边上的点F处.