题目内容
19.若关于x,y的方程组$\left\{\begin{array}{l}{y=kx-1}\\{y={x}^{2}+x}\end{array}\right.$有唯一解,则k的值是-1或3.分析 把①代入②,得到关于x的一元二次方程,根据判别式为0时方程有两个相等的实根,列出方程求出k即可.
解答 解:$\left\{\begin{array}{l}{y=kx-1①}\\{y={x}^{2}+x②}\end{array}\right.$
把①代入②得,
kx-1=x2+x,
整理得,x2+(1-k)x+1=0
使方程有唯一解,判别式为0,
(1-k)2-4=0,
解得k1=-1,k2=3.
故答案为:-1或3.
点评 本题考查的是二元二次方程的解的判断,步骤是把方程组通过代入法化为一元二次方程,然后根据一元二次方程根的判别式进行判断.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
4. 如图,⊙O是△ABC的外接圆,已知∠A=30°,BC=2,则⊙O的半径为( )
如图,⊙O是△ABC的外接圆,已知∠A=30°,BC=2,则⊙O的半径为( )
 如图,⊙O是△ABC的外接圆,已知∠A=30°,BC=2,则⊙O的半径为( )
如图,⊙O是△ABC的外接圆,已知∠A=30°,BC=2,则⊙O的半径为( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 4 |
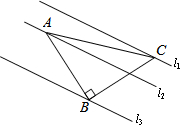 如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为7,l2,l3之间的距离为8,求AC的长.
如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为7,l2,l3之间的距离为8,求AC的长.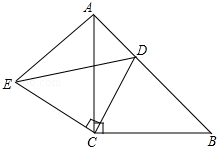 已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB边上一点.猜想BD2、AD2、CD2之间的关系,并证明.
已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB边上一点.猜想BD2、AD2、CD2之间的关系,并证明.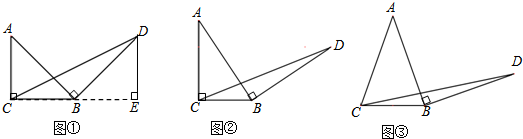
 如图所示,AB,CD相交于O点,OE是∠COB的平分线,FO⊥OE,且∠AOD=60°.
如图所示,AB,CD相交于O点,OE是∠COB的平分线,FO⊥OE,且∠AOD=60°.