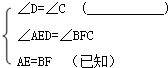题目内容
10.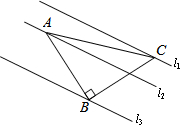 如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为7,l2,l3之间的距离为8,求AC的长.
如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为7,l2,l3之间的距离为8,求AC的长.
分析 过A、C点作l3的垂线构造出直角三角形,根据三角形全等求出BE=AD=3,由勾股定理求出BC的长,再利用勾股定理即可求出.
解答 解:作AD⊥l3于D,作CE⊥l3于E,
∵∠ABC=90°,
∴∠ABD+∠CBE=90°
又∠DAB+∠ABD=90°
∴∠BAD=∠CBE,
在△ABD和△BEC中,
$\left\{\begin{array}{l}{∠ADB=BEC}\\{∠BAD=∠EBC}\\{AB=BC}\end{array}\right.$,
∴△ABD≌△BCE(AAS),
∴BE=AD=8,
在Rt△BCE中,根据勾股定理,得BC=$\sqrt{{CE}^{2}{+BE}^{2}}$=$\sqrt{{15}^{2}{+8}^{2}}$=17,
在Rt△ABC中,根据勾股定理,得AC=$\sqrt{{AB}^{2}{+BC}^{2}}$=$\sqrt{{17}^{2}{+17}^{2}}$=17$\sqrt{2}$.
点评 本题考查了全等三角形的性质和判定,勾股定理的应用,此题要作出平行线间的距离,构造直角三角形.运用全等三角形的判定和性质以及勾股定理进行计算.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
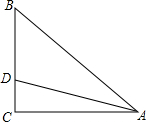 如图,在Rt△ABC中,∠C=90°,AB=10,tanB=$\frac{4}{3}$,CD=2,求△ABD的周长.
如图,在Rt△ABC中,∠C=90°,AB=10,tanB=$\frac{4}{3}$,CD=2,求△ABD的周长.
 如图,在△ABC中,∠BAC=90°,AB=AC=6,D为BC的中点.若E、F分别是AB、AC上的点,且AE=CF.
如图,在△ABC中,∠BAC=90°,AB=AC=6,D为BC的中点.若E、F分别是AB、AC上的点,且AE=CF.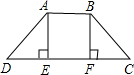 如图,四边形ABCD是一防洪堤坝的横截面,AE⊥CD,BF⊥CD,且AE=BF,∠D=∠C,问AD与BC是否相等?说明你的理由.
如图,四边形ABCD是一防洪堤坝的横截面,AE⊥CD,BF⊥CD,且AE=BF,∠D=∠C,问AD与BC是否相等?说明你的理由.