��Ŀ����
14������ԭ�ͣ���ͼ�٣��ڵ���ֱ��������ABC�У���ACB=90�㣬BC=a������AB�Ƶ�B˳ʱ����ת90��õ��߶�BD������CD������D����BCD��BC���ϵĸ�DE����֤��ABC�ա�BDE���Ӷ��õ���BCD�����Ϊ$\frac{1}{2}{a^2}$��
����̽������ͼ�ڣ���Rt��ABC�У���ACB=90�㣬BC=a������AB�Ƶ�B˳ʱ����ת90��õ��߶�BD������CD���ú�a�Ĵ���ʽ��ʾ��BCD���������˵�����ɣ�
��Ӧ�ã���ͼ�ۣ��ڵ���������ABC�У�AB=AC��BC=a������AB�Ƶ�B˳ʱ����ת90��õ��߶�BD������CD��ֱ��д����BCD����������ú�a�Ĵ���ʽ��ʾ��
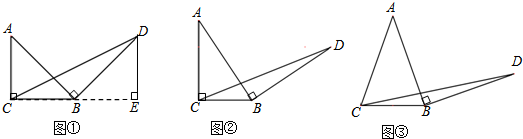
���� ����̽������ͼ�ڣ�����D��BC�Ĵ��ߣ���BC���ӳ��߽��ڵ�E���ɴ�ֱ�����ʾͿ��Եó���ABC�ա�BDE������DE=BC=a�������������ε������ʽ�ó����ۣ�
�����ã���ͼ�ۣ�����A��AF��BC��F������D��DE��BC���ӳ����ڵ�E���ɵ��������ε����ʿ��Եó�BF=$\frac{1}{2}$BC�����������Եó���AFB�ա�BED�Ϳ��Եó�BF=DE���������ε������ʽ�Ϳ��Եó����ۣ�
��� �⣺����̽������BCD�����Ϊ$\frac{1}{2}{a^2}$��
���ɣ���ͼ�ڣ�����D��BC�Ĵ��ߣ���BC���ӳ��߽��ڵ�E��
���BED=��ACB=90�㣮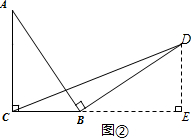
���߶�AB�Ƶ�B˳ʱ����ת90��õ��߶�BE��
��AB=BD����ABD=90�㣮
���ABC+��DBE=90�㣮
�ߡ�A+��ABC=90�㣮
���A=��DBE��
�ڡ�ABC�͡�BDE�У�
$\left\{\begin{array}{l}{��ACB=��BED}\\{��A=��DBE}\\{AB=BD}\end{array}\right.$��
���ABC�ա�BDE��AAS��
��BC=DE=a��
��S��BCD=$\frac{1}{2}$BC•DE
��S��BCD=$\frac{1}{2}{a^2}$��
��Ӧ�ã���ͼ�ۣ�����A��AF��BC��F������D��DE��BC���ӳ����ڵ�E��
���AFB=��E=90�㣬BF=$\frac{1}{2}$BC=$\frac{1}{2}$a��
���FAB+��ABF=90�㣮
�ߡ�ABD=90�㣬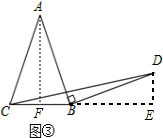
���ABF+��DBE=90�㣬
���FAB=��EBD��
���߶�BD�����߶�AB��ת�õ��ģ�
��AB=BD��
�ڡ�AFB�͡�BED�У�
$\left\{\begin{array}{l}{��AFB=��E}\\{��FAB=��EBD}\\{AB=BD}\end{array}\right.$��
���AFB�ա�BED��AAS����
��BF=DE=$\frac{1}{2}$a��
��S��BCD=$\frac{1}{2}$BC•DE��
��S��BCD=$\frac{1}{2}$•$\frac{1}{2}$a•a=$\frac{1}{4}$a2��
���BCD�����Ϊ$\frac{1}{4}{a^2}$��
���� ���⿼����ֱ�������ε����ʵ����ã����������ε����ʵ����ã�ȫ�������ε��ж������ʵ����ã������ε������ʽ�����ã����ʱ֤��������ȫ���ǹؼ���

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | -2 | B�� | -1 | C�� | 1 | D�� | 2 |
| A�� | 3a+3b=6ab | B�� | a3-a=a2 | C�� | ��a2��3=a6 | D�� | a6��a3=a2 |
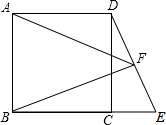 ��ͼ����EΪ������ABCD�ı�BC�ӳ�����һ�㣬����DE����FΪ�߶�DE��һ�㣬����AF��BF��AF����ƽ�֡�DFB��
��ͼ����EΪ������ABCD�ı�BC�ӳ�����һ�㣬����DE����FΪ�߶�DE��һ�㣬����AF��BF��AF����ƽ�֡�DFB�� ��ͼ���ڡ�ABC�У���BAC=90�㣬AB=AC=6��DΪBC���е㣮��E��F�ֱ���AB��AC�ϵĵ㣬��AE=CF��
��ͼ���ڡ�ABC�У���BAC=90�㣬AB=AC=6��DΪBC���е㣮��E��F�ֱ���AB��AC�ϵĵ㣬��AE=CF��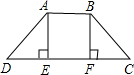 ��ͼ���ı���ABCD��һ����̰ӵĺ���棬AE��CD��BF��CD����AE=BF����D=��C����AD��BC�Ƿ���ȣ�˵��������ɣ�
��ͼ���ı���ABCD��һ����̰ӵĺ���棬AE��CD��BF��CD����AE=BF����D=��C����AD��BC�Ƿ���ȣ�˵��������ɣ�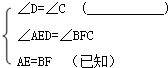
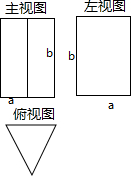 һ�������������ͼ��ͼ��ʾ����֪����ͼ������ͼ����ͼ��ͼ��ʾ��
һ�������������ͼ��ͼ��ʾ����֪����ͼ������ͼ����ͼ��ͼ��ʾ��