题目内容
11.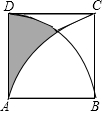 如图,正方形ABCD的边长为6,分别以A、B为圆心,6为半径画$\widehat{BD}$、$\widehat{AC}$,则图中阴影部分的面积为9$\sqrt{3}$-3π.
如图,正方形ABCD的边长为6,分别以A、B为圆心,6为半径画$\widehat{BD}$、$\widehat{AC}$,则图中阴影部分的面积为9$\sqrt{3}$-3π.
分析 如解答图,作辅助线,利用图形的对称性求解.
解答  解:如图:
解:如图:
阴影部分的面积=S正方形ABCD-S扇形ABC-2(长方形AFED的面积-扇形DAG的面积-三角形AGF的面积)=36-$\frac{90•π×{6}^{2}}{360}$-2(3×6-$\frac{30•π×{6}^{2}}{360}$-$\frac{1}{2}×$3×3$\sqrt{3}$)=9$\sqrt{3}$-3π,
故答案为:9$\sqrt{3}$-3π.
点评 本题考查了扇形的面积公式和长方形性质的应用,关键是根据用图形的对称性分析,主要考查学生的计算能力.

练习册系列答案
相关题目
2.在?ABCD中,对角线AC、BD相交于点O,若BC=12,则AC与BD的值可能是( )
| A. | 8和14 | B. | 10和14 | C. | 10和34 | D. | 18和20 |
1.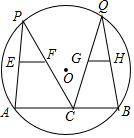 如图,P、Q两点是半径为2cm的⊙O上的两动点,E、F分别是弦PA、PC的中点,G、H分别是弦QC、QB的中点,则EF+GH的值( )
如图,P、Q两点是半径为2cm的⊙O上的两动点,E、F分别是弦PA、PC的中点,G、H分别是弦QC、QB的中点,则EF+GH的值( )
 如图,P、Q两点是半径为2cm的⊙O上的两动点,E、F分别是弦PA、PC的中点,G、H分别是弦QC、QB的中点,则EF+GH的值( )
如图,P、Q两点是半径为2cm的⊙O上的两动点,E、F分别是弦PA、PC的中点,G、H分别是弦QC、QB的中点,则EF+GH的值( )| A. | 随着P、Q的运动而变化 | |
| B. | 等于2cm | |
| C. | P、Q两点在弦AB同侧时,EF+GH为定值,在AB异侧时不为定值 | |
| D. | 等于AB的一半 |
 如图,已知点O为平行四边形ABCD所在平面上一点,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,求$\overrightarrow{OD}$(用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示)
如图,已知点O为平行四边形ABCD所在平面上一点,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,求$\overrightarrow{OD}$(用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示)