题目内容
6.(1)解不等式组$\left\{\begin{array}{l}{3(x+1)>4x+2}\\{\frac{x}{2}>\frac{x-1}{3}}\end{array}\right.$,并写出不等式组的整数解.(2)化简分式:($\frac{3x}{x-1}$-$\frac{x}{x+1}$)÷$\frac{x}{{x}^{2}-1}$,再从-2<x<3的范围内选取一个你最喜欢的值代入求值.
分析 (1)根据解不等式组的方法可以求得不等式组的解集,从而可以得到不等式组的整数解;
(2)先化简题目中的式子,然后在-2<x<3的范围内选取一个使得原分式有意义的x的值代入即可解答本题.
解答 解:(1)$\left\{\begin{array}{l}{3(x+1)>4x+2}&{①}\\{\frac{x}{2}>\frac{x-1}{3}}&{②}\end{array}\right.$,
解不等式①,得
x<1,
解不等式②,得
x>-2,
由不等式①②可得,原不等式组的解集是-2<x<1,
∴不等式组的整数解是:x=-1,0;
(2)($\frac{3x}{x-1}$-$\frac{x}{x+1}$)÷$\frac{x}{{x}^{2}-1}$
=$\frac{3x(x+1)-x(x-1)}{(x-1)(x+1)}•\frac{(x+1)(x-1)}{x}$
=3(x+1)-(x-1)
=3x+3-x+1
=2x+4,
当x=2时,原式=2×2+4=8.
点评 本题考查分式的化简求值、解一元一次不等式组、一元一次不等式组的整数解,解答本题的关键是明确它们各自的计算方法.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
1.据统计,2017年高新技术产品出口总额达50570亿元,将数据50570亿用科学记数法表示为( )
| A. | 5.0570×109 | B. | 0.50570×1010 | C. | 50.570×1011 | D. | 5.0570×1012 |
18.已知:菱形的边长为4,且有一个内角为60°,一条直线将菱形ABCD分成面积相等的两个图形,设该直线与菱形的边交于点E,F,则线段EF的长m的取值范围( )
| A. | m=4或m=4$\sqrt{3}$ | B. | 4≤m≤4$\sqrt{3}$ | C. | 2$\sqrt{3}$≤m≤4$\sqrt{3}$ | D. | 2$\sqrt{3}$≤m≤4 |
 如图,将矩形纸片ABCD折叠,使点C与点A重合,折痕EF分别与AB、DC交于点E和点F.
如图,将矩形纸片ABCD折叠,使点C与点A重合,折痕EF分别与AB、DC交于点E和点F. 如图,在△ABC中,点D,E分别是AC、AB上的中点,BD与CE相交于点O.求证:OC=2OE.
如图,在△ABC中,点D,E分别是AC、AB上的中点,BD与CE相交于点O.求证:OC=2OE. 星期天的早晨,小明骑自行车从家出发,到离家1050米的书店买书,出发1分钟后,他到达离家150米的地方,又过1分钟后,小明加快了速度.如图所示是小明从家出发后离家的路程y(米)与他骑自行车的时间x(分钟)之间的函数图象.根据图象解答下列问题:
星期天的早晨,小明骑自行车从家出发,到离家1050米的书店买书,出发1分钟后,他到达离家150米的地方,又过1分钟后,小明加快了速度.如图所示是小明从家出发后离家的路程y(米)与他骑自行车的时间x(分钟)之间的函数图象.根据图象解答下列问题: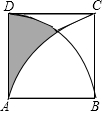 如图,正方形ABCD的边长为6,分别以A、B为圆心,6为半径画$\widehat{BD}$、$\widehat{AC}$,则图中阴影部分的面积为9$\sqrt{3}$-3π.
如图,正方形ABCD的边长为6,分别以A、B为圆心,6为半径画$\widehat{BD}$、$\widehat{AC}$,则图中阴影部分的面积为9$\sqrt{3}$-3π.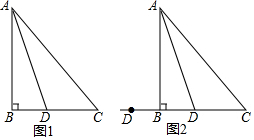 在△ABC中,AB=BC,∠B=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.
在△ABC中,AB=BC,∠B=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.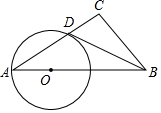 如图,Rt△ABC中∠C=90°,点O是AB边上一点,以OA为半径作⊙O,与边AC交于点D,连接BD,若∠DBC=∠A,求证:BD是⊙O的切线.
如图,Rt△ABC中∠C=90°,点O是AB边上一点,以OA为半径作⊙O,与边AC交于点D,连接BD,若∠DBC=∠A,求证:BD是⊙O的切线.