题目内容
20.圆锥体的底面周长为6π,侧面积为15π,则该圆锥体的高为4.分析 让周长除以2π即为圆锥的底面半径;根据圆锥的侧面积=$\frac{1}{2}$×侧面展开图的弧长×母线长可得圆锥的母线长,利用勾股定理可得圆锥的高.
解答 解:∵圆锥的底面周长为6π,
∴圆锥的底面半径为6π÷2π=3,
∵圆锥的侧面积=$\frac{1}{2}$×侧面展开图的弧长×母线长,
∴母线长=2×15π÷(6π)=5,
∴这个圆锥的高是$\sqrt{{5}^{2}-{3}^{2}}$=4,
故答案为:4.
点评 考查圆锥的计算,用到的知识点为:圆锥的底面周长等于侧面展开图的弧长;圆锥的侧面积=$\frac{1}{2}$×侧面展开图的弧长×母线长.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
5.位于武侯区“中国女鞋之都”的某制鞋企业为了了解初中学生穿鞋的尺码情况,选择对某校的40名女生进行了调查,结果如下表所示,那么在平均数、中位数、众数三个统计量中,该制鞋企业最感兴趣的统计量是众数,该统计量的数值是36码.
| 尺码(单位:码) | 33 | 34 | 35 | 36 | 37 | 38 |
| 人数 | 2 | 8 | 8 | 14 | 6 | 2 |
12. 如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥底面半径r=2,扇形圆心角θ=120°,则该圆锥母线长为( )
如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥底面半径r=2,扇形圆心角θ=120°,则该圆锥母线长为( )
 如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥底面半径r=2,扇形圆心角θ=120°,则该圆锥母线长为( )
如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥底面半径r=2,扇形圆心角θ=120°,则该圆锥母线长为( )| A. | 10 | B. | $\frac{15}{2}$ | C. | 6 | D. | 8 |
9.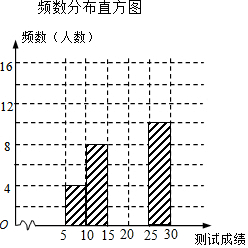 某校为了调查初一年级学生有理数混合运算能力,从七年级400名学生中堆积抽选50名学生参加测试,对这50名学生同时进行30个有理数混合运算的考察,每做正确1个得1分,根据测试成绩绘制出不完整的频数分布直方图如下图表:
某校为了调查初一年级学生有理数混合运算能力,从七年级400名学生中堆积抽选50名学生参加测试,对这50名学生同时进行30个有理数混合运算的考察,每做正确1个得1分,根据测试成绩绘制出不完整的频数分布直方图如下图表:
频数分布表
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于15分为合格,请你估计该校七年级学生有理数混合运算能力测试合格的人数?
 某校为了调查初一年级学生有理数混合运算能力,从七年级400名学生中堆积抽选50名学生参加测试,对这50名学生同时进行30个有理数混合运算的考察,每做正确1个得1分,根据测试成绩绘制出不完整的频数分布直方图如下图表:
某校为了调查初一年级学生有理数混合运算能力,从七年级400名学生中堆积抽选50名学生参加测试,对这50名学生同时进行30个有理数混合运算的考察,每做正确1个得1分,根据测试成绩绘制出不完整的频数分布直方图如下图表:频数分布表
| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 5≤x<10 | 4 |
| 第2组 | 10≤x<15 | 8 |
| 第3组 | 15≤x<20 | 16 |
| 第4组 | 20≤x<25 | a |
| 第5组 | 25≤x<30 | b |
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于15分为合格,请你估计该校七年级学生有理数混合运算能力测试合格的人数?
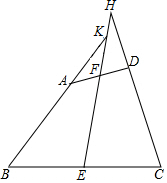 如图,在四边形ABCD中,AB=CD,E,F分别是BC,AD的中点,延长BA和CD分别与EF的延长线交于K,H.求证:∠BKE=∠CHE.
如图,在四边形ABCD中,AB=CD,E,F分别是BC,AD的中点,延长BA和CD分别与EF的延长线交于K,H.求证:∠BKE=∠CHE.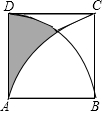 如图,正方形ABCD的边长为6,分别以A、B为圆心,6为半径画$\widehat{BD}$、$\widehat{AC}$,则图中阴影部分的面积为9$\sqrt{3}$-3π.
如图,正方形ABCD的边长为6,分别以A、B为圆心,6为半径画$\widehat{BD}$、$\widehat{AC}$,则图中阴影部分的面积为9$\sqrt{3}$-3π.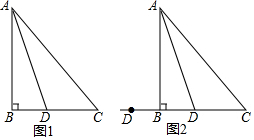 在△ABC中,AB=BC,∠B=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.
在△ABC中,AB=BC,∠B=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.