题目内容
13.已知a、b、c为整数,且a2+b2+c2-ab-bc-ac=19,那么a+b+c的最小值等于( )| A. | 11 | B. | 10 | C. | 8 | D. | 6 |
分析 利用配方法得到(a-b)2+(b-c)2+(c-a)2=38,由于02=0,12=1,22=4,32=9,42=16,52=25,62=36,则22+32+52=38,于是可判断a-b、b-c、c-a为±2,±3,±5中的任意一组值,然后分别列方程组求出a、b、c的值,再判断a+b+c的最小值.
解答 解:∵a2+b2+c2-ab-bc-ac=19,
∴2a2+2b2+2c2-2ab-2bc-2ac=38,
∴(a-b)2+(b-c)2+(c-a)2=38,
∵a、b、c为整数,
∴a-b、b-c、c-a为整数,
而02=0,12=1,22=4,32=9,42=16,52=25,62=36,
∴22+32+52=38,
∴a-b、b-c、c-a为±2,±3,±5中的任意一组值,
若a-b=2,b-c=3,c-a=5,解得a=6,b=4,c=1,则a+b+c=11,
若a-b=-2,b-c=-3,c-a=5,解得a=1,b=3,c=6,则a+b+c=10,
通过计算可得+b+c的最小值为10.
故选B.
点评 本题考查了因式分解的应用:利用因式分解解决求值问题;利用因式分解解决证明问题;利用因式分解简化计算问题.也考查了非负数的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5. 如图,AB=CD=3,∠A=75°,∠B=45°,∠D=15°,则线段AD的长为( )
如图,AB=CD=3,∠A=75°,∠B=45°,∠D=15°,则线段AD的长为( )
 如图,AB=CD=3,∠A=75°,∠B=45°,∠D=15°,则线段AD的长为( )
如图,AB=CD=3,∠A=75°,∠B=45°,∠D=15°,则线段AD的长为( )| A. | 4 | B. | 2$\sqrt{5}$ | C. | 2$\sqrt{6}$ | D. | 2$\sqrt{7}$ |
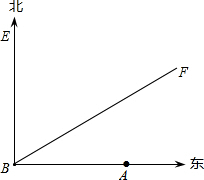 如图,A城气象台刻得台风中心在A城正西方向160km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心100km的范围内是受台风影响的区域.
如图,A城气象台刻得台风中心在A城正西方向160km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心100km的范围内是受台风影响的区域.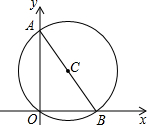 如图,⊙C经过原点O且与两坐标轴分别交于点A和点B,点A的坐标为(0,2),点B的坐标为(2$\sqrt{3}$,0).
如图,⊙C经过原点O且与两坐标轴分别交于点A和点B,点A的坐标为(0,2),点B的坐标为(2$\sqrt{3}$,0).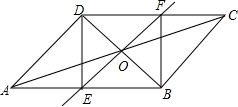 如图,已知平行四边形ABCD的对角线AC、BD相交于点O,BD绕点O顺时针旋转交AB于F、E,请你判断BD绕点O顺时针旋转多少度时,四边形BFDE为菱形?请说明理由.
如图,已知平行四边形ABCD的对角线AC、BD相交于点O,BD绕点O顺时针旋转交AB于F、E,请你判断BD绕点O顺时针旋转多少度时,四边形BFDE为菱形?请说明理由.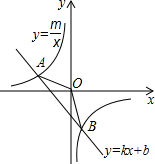 如图,已知A(-4,2),B(n,-4)是一次函数y1=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点;
如图,已知A(-4,2),B(n,-4)是一次函数y1=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点; 如图,正方形ABCD和正方形CEFG有公共顶点C,点C的坐标是C(6,4),点B,E,F在x轴上,点A在y轴上,反比例函数y=$\frac{k}{x}$的图象经过CE的中点Q.
如图,正方形ABCD和正方形CEFG有公共顶点C,点C的坐标是C(6,4),点B,E,F在x轴上,点A在y轴上,反比例函数y=$\frac{k}{x}$的图象经过CE的中点Q.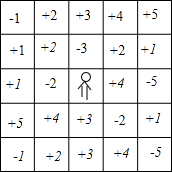 如图是一个“冲出围城”的游戏,规则是:城中人想要冲出围城,可以横走也可以竖走,但不可以斜走,每走一格就可以得到格中相应的分数作为生命值,每格中的分数用乘法累计.当生命值小于+9,并且处于最外圈时,就可以冲出围城,生命值为负数不可以出城.例如:(-2)×(+2)×(+2)×(-1)=+8,就是一条冲出围城的路线.把你找到的冲出围城的路线写下来,也可以直接用箭头将路线在表中表示出来.
如图是一个“冲出围城”的游戏,规则是:城中人想要冲出围城,可以横走也可以竖走,但不可以斜走,每走一格就可以得到格中相应的分数作为生命值,每格中的分数用乘法累计.当生命值小于+9,并且处于最外圈时,就可以冲出围城,生命值为负数不可以出城.例如:(-2)×(+2)×(+2)×(-1)=+8,就是一条冲出围城的路线.把你找到的冲出围城的路线写下来,也可以直接用箭头将路线在表中表示出来.