题目内容
8.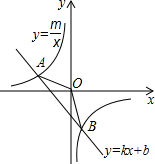 如图,已知A(-4,2),B(n,-4)是一次函数y1=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点;
如图,已知A(-4,2),B(n,-4)是一次函数y1=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点;(1)求反比例函数和一次函数的关系式;
(2)在反比例函数中,当y>-4时,求x的取值范围;并求当-2<x<-1时,y的范围;
(3)根据图象直接写出不等式kx+b-$\frac{m}{x}$≥0的解集;
(4)在x轴上是否存在点Q使得△OAQ是等腰三角形,写出点Q的坐标;
(5)反向延长OA交反比例函数于点C,反向延长OB交反比例函数于点D,则四边形ABCD是什么四边形?不必证明;
(6)在双曲线上有一点M的横坐标为-1,连接MA、OM,求出△OAM的面积.
分析 (1)先把AB两点代入反比例函数的解析式求出m、n的值,再代入一次函数的解析式即可;
(2)直接根据一次函数与反比例函数在坐标系中的图象即可得出结论;
(3)直接根据函数的图象即可得出结论;
(4)分OA=QA,OA=OQ及QA=OQ三种情况进行讨论;
(5)直接根据平行四边形的判定定理即可得出结论;
(6)先求出M的坐标,点M作ME⊥y轴于点E,AD⊥y轴于点D,AF⊥x轴于点F,根据S△OAM=S梯形ADEM+S矩形AFOD-S△MEO-S△AOF即可得出结论.
解答 解:(1)∵点A(-4,2)和点B(n,-4)都在反比例函数y=$\frac{m}{x}$的图象上,
∴$\left\{\begin{array}{l}2=\frac{m}{-4}\\-4=\frac{m}{n}\end{array}\right.$,
解得 $\left\{\begin{array}{l}m=-8\\ n=2\end{array}\right.$.
又由点A(-4,2)和点B(2,-4)都在一次函数y=kx+b的图象上,
∴$\left\{\begin{array}{l}-4k+b=2\\ 2k+b=-4\end{array}\right.$,
解得 $\left\{\begin{array}{l}k=-1\\ b=-2\end{array}\right.$.
∴反比例函数的解析式为y=-$\frac{8}{x}$,一次函数的解析式为y=-x-2;
(2)由图象可知,当y>-4时,0<x<2或x<0;
当-2<x<-1时,4<y<8;
(3)∵kx+b-$\frac{m}{x}$≥0,
∴kx+b≥$\frac{m}{x}$,
由函数图象可知,当0<x≤2或x≤-4时,kx+b-$\frac{m}{x}$≥0;
(4)∵A(-4,2),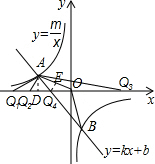
∴OA=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$.
如图所示,当OA=QA时,过点A作AD⊥x轴于点D,则OD=QD,
∵A(-4,2),
∴Q1(-8,0);
当OA=OQ时,
∵A(-4,2),
∴OA=$\sqrt{(-4)^{2}+{2}^{2}}$=2$\sqrt{5}$
∴Q2(2$\sqrt{5}$,0),Q3(-2$\sqrt{5}$,0);
当QA=OQ时,设Q(x,0),则$\sqrt{(-4-x)^{2}+{2}^{2}}$=-x,解得x=-$\frac{5}{2}$
.∴Q4(-$\frac{5}{2}$,0).
综上所示,Q1(-8,0),Q2(2$\sqrt{5}$,0),Q3(-2$\sqrt{5}$,0),Q4(-$\frac{5}{2}$,0);
(5)∵反比例函数图象上的点关于原点O对称,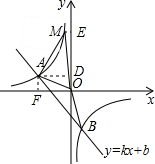
∴OA=OC,OB=OD,
∴四边形ABCD是平行四边形;
(6)如图,
∵反比例函数的解析式为y=-$\frac{8}{x}$,
∴当x=-1时,y=8,即M(-1,8).
过点M作ME⊥y轴于点E,AD⊥y轴于点D,AF⊥x轴于点F,
则S△OAM=S梯形ADEM+S矩形AFOD-S△MEO-S△AOF
=$\frac{1}{2}$(1+4)×6+4×2-$\frac{1}{2}$×1×6-$\frac{1}{2}$×4×2
=15+8-3-4
=16.
点评 本题考查的是反比例函数综合题,涉及到反比例函数与一次函数的交点问题,三角形的面积等知识,在解答(4)时要注意进行分类讨论.

| A. | 2$\frac{1}{3}$ | B. | -2$\frac{1}{3}$ | C. | 0 | D. | $\frac{2}{3}$ |
| A. | 8 | B. | 1 | C. | -1或8 | D. | -1或1 |
| A. | 11 | B. | 10 | C. | 8 | D. | 6 |
| A. | 3a2b | B. | $\frac{1}{2}$b2a | C. | 2ab3 | D. | 3a2b2 |
