题目内容
1.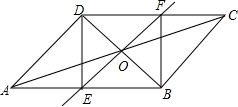 如图,已知平行四边形ABCD的对角线AC、BD相交于点O,BD绕点O顺时针旋转交AB于F、E,请你判断BD绕点O顺时针旋转多少度时,四边形BFDE为菱形?请说明理由.
如图,已知平行四边形ABCD的对角线AC、BD相交于点O,BD绕点O顺时针旋转交AB于F、E,请你判断BD绕点O顺时针旋转多少度时,四边形BFDE为菱形?请说明理由.
分析 根据平行四边形的性质得出OD=OB,DC∥AB,推出∠FDO=∠EBO,证出△DFO≌△BEO,从而得到OE=OF,然后可证明四边形EBFD为平行四边形,最后根据对角线相互垂直的平行四边形是菱形解答即可.
解答 解:当∠DOE=90°时,四边形BFDE为菱形.
理由:∵四边形ABCD是平行四边形,
∴OD=OB,DC∥AB,
∴∠FDO=∠EBO,
在△DFO和△BEO中,
$\left\{\begin{array}{l}{∠FDO=∠EBO}\\{OD=OB}\\{∠FOD=∠EOB}\end{array}\right.$,
∴△DFO≌△BEO(ASA),
∴OE=OF.
又∵OD=OB,
∴四边形EBFD为平行四边形.
∵∠DOE=90°,
∴四边形BFDE为菱形.
点评 本题主要考查的是平行四边形的性质和判定、菱形的判定、全等三角形的判定,掌握菱形的判定定理是解题的关键.

练习册系列答案
相关题目
13.已知a、b、c为整数,且a2+b2+c2-ab-bc-ac=19,那么a+b+c的最小值等于( )
| A. | 11 | B. | 10 | C. | 8 | D. | 6 |
 请阅读下面材料:
请阅读下面材料:
 如图,在平面直角坐标系中,反比例函数y1=$\frac{k_1}{x}$(x>0)的图象与y2=$\frac{k_2}{x}$(x>0)的图象关于x轴对称,Rt△AOB的顶点A,B分别在y1=$\frac{k_1}{x}$(x>0)和y2=$\frac{k_2}{x}$(x>0)的图象上.若OB=AB,点B的纵坐标为-2,则点A的坐标为(1+$\sqrt{5}$,3-$\sqrt{5}$).
如图,在平面直角坐标系中,反比例函数y1=$\frac{k_1}{x}$(x>0)的图象与y2=$\frac{k_2}{x}$(x>0)的图象关于x轴对称,Rt△AOB的顶点A,B分别在y1=$\frac{k_1}{x}$(x>0)和y2=$\frac{k_2}{x}$(x>0)的图象上.若OB=AB,点B的纵坐标为-2,则点A的坐标为(1+$\sqrt{5}$,3-$\sqrt{5}$).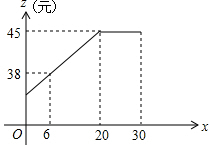 大学生李某毕业响应国家“自主创业”的号召,在我市沙坪坝学校密集的沙南街路段投资开办了一个学生文具店.该店在开学前8月31日购进一种今年新上市的文具袋9月份(9月1日至9月30日)进行30天的试销售,购进价格为20元/个.销售结束后得知日销售量y(个)与销售时间x(天)之间有如下关系:y=-2x+80(1≤x≤30,x取正整数);又知销售价格z(元/个)与销售时间x(天,x取正整数)之间的函数关系满足如图所示的函数图象.
大学生李某毕业响应国家“自主创业”的号召,在我市沙坪坝学校密集的沙南街路段投资开办了一个学生文具店.该店在开学前8月31日购进一种今年新上市的文具袋9月份(9月1日至9月30日)进行30天的试销售,购进价格为20元/个.销售结束后得知日销售量y(个)与销售时间x(天)之间有如下关系:y=-2x+80(1≤x≤30,x取正整数);又知销售价格z(元/个)与销售时间x(天,x取正整数)之间的函数关系满足如图所示的函数图象.