题目内容
10.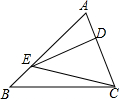 如图,在△ABC中,点D为AC上一点,点E为AB上一点,若AB=4,AD:DC=1:2且S△DEC=$\frac{1}{2}$S△ABC,则EB的长为( )
如图,在△ABC中,点D为AC上一点,点E为AB上一点,若AB=4,AD:DC=1:2且S△DEC=$\frac{1}{2}$S△ABC,则EB的长为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
分析 由已知AD=1,DC=2,得△DEC的面积等于△AED面积的2倍,又由△ABC的面积等于△DEC面积的2倍,得出△ABC的面积等于△BCE面积的4倍,计算△ABC的面积、△BCE面积用AB和EB为底,则两三角形的高相等,则得出BE与AB的关系,从而求出BE的长.
解答 解:已知AD=1,DC=2,
∴S△DEC=2S△AED,
又由S△ABC=2S△DEC,
∵S△BCE+S△AED+S△DEC=S△ABC,
∴S△BCE+$\frac{1}{2}$S△DEC+S△DEC=2S△DEC,
∴S△BCE=$\frac{1}{2}$S△DEC=$\frac{1}{4}$S△ABC,
设△ABC和△BCE的同高为h,
则:$\frac{1}{2}$BE•h=$\frac{1}{4}$×$\frac{1}{2}$AB•h,
∴BE=$\frac{1}{4}$AB=$\frac{1}{4}$×4=1.
故选B.
点评 此题考查的知识点是三角形的面积,关键是由已知先得出△DEC的面积等于△AED面积的2倍,然后由面积关系得出BE=$\frac{1}{4}$AB.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
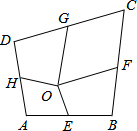 如图所示,四边形ABCD中,E、F、G、H依次是各边中点,O是四边形形内一点,若
如图所示,四边形ABCD中,E、F、G、H依次是各边中点,O是四边形形内一点,若 按如图所示的程序计算,若开始输入的x的值为12,我们发现第一次得到的结果为6,第2次得到的结果为3,…,请你探索第2011次得到的结果为6.
按如图所示的程序计算,若开始输入的x的值为12,我们发现第一次得到的结果为6,第2次得到的结果为3,…,请你探索第2011次得到的结果为6. 如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠E=45°,直线CD是否与⊙O相切?为什么?
如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠E=45°,直线CD是否与⊙O相切?为什么? 如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,有下面3个结论:①BD是∠ABC的角平分线;②△BCD是等腰三角形;③△AMD≌△BCD.
如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,有下面3个结论:①BD是∠ABC的角平分线;②△BCD是等腰三角形;③△AMD≌△BCD.