题目内容
2．在平面直角坐标系中，有一点P，若将P先向右平移5个单位长度，再向上平移3个单位长度，所得坐标为（-3，9），则P坐标为（-8，6）．分析 根据向右平移，横坐标加，向上平移，纵坐标加进行计算即可得解．
解答 解：设点P坐标为（x，y）．
∵将P先向右平移5个单位长度，再向上平移3个单位长度，所得坐标为（-3，9），
∴x+5=-3，y+3=9，
∴x=-8，y=6，
∴点P坐标为（-8，6）．
故答案为（-8，6）．
点评 本题考查了坐标与图形的变化-平移，熟记平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减是解题的关键．
练习册系列答案
相关题目
10．
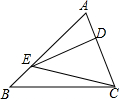如图，在△ABC中，点D为AC上一点，点E为AB上一点，若AB=4，AD：DC=1：2且S△DEC=$\frac{1}{2}$S△ABC，则EB的长为（ ）
如图，在△ABC中，点D为AC上一点，点E为AB上一点，若AB=4，AD：DC=1：2且S△DEC=$\frac{1}{2}$S△ABC，则EB的长为（ ）| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{3}{2}$ | D． | 2 |
△ABC在平面直角坐标系xOy中的位置如图所示．
12．下列运算中，正确的是（ ）
| A． | $\sqrt{{a}^{2}}$=a | B． | $\frac{-a-b}{a+b}$=1 | C． | $\sqrt{（-4）^{2}}$=4 | D． | $\frac{x-y}{x+y}=\frac{y-x}{y+x}$ |