题目内容
15. 如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,有下面3个结论:①BD是∠ABC的角平分线;②△BCD是等腰三角形;③△AMD≌△BCD.
如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,有下面3个结论:①BD是∠ABC的角平分线;②△BCD是等腰三角形;③△AMD≌△BCD.其中正确的结论有①②(只需填写正确结论的序号).
分析 由AB=AC,∠A=36°,根据等腰三角形的性质,可求得∠ABC与∠C的度数,又由AB的中垂线MN交AC于点D、交AB于点M,可求得∠ABD的度数,继而可得BD是∠ABC的平分;△BCD是等腰三角形;
解答 解:∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵AB的中垂线MN交AC于点D、交AB于点M,
∴AD=BD,
∴∠ABD=∠A=36°,
∴∠DBC=∠ABC-∠ABD=36°,
∴∠ABD=∠CBD,
即BD是∠ABC的平分线,故①正确;
∵∠BDC=∠A+∠ABD=72°,
∴∠BDC=∠C,
∴BD=BC,
∴△BCD是等腰三角形;故②正确;
∵AM⊥MD,而△BCD为锐角三角形,
∴③错误,
故答案为:①②.
点评 此题考查了线段垂直平分线的性质以及等腰三角形的性质.注意垂直平分线上任意一点,到线段两端点的距离相等定理的应用.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
5.已知a<b<0,则下列式子中成立的是( )
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | ab<1 | C. | $\frac{a}{b}$<1 | D. | $\frac{a}{b}$>1 |
6.下列说法错误的是( )
| A. | 在一个角的内部(包括顶点)到角的两边距离相等的点的轨迹是这个角的平分线 | |
| B. | 到点P距离等于1 cm的点的轨迹是以点P为圆心,半径长为1cm的圆 | |
| C. | 到直线l距离等于2 cm的点的轨迹是两条平行于l且与l的距离等于2cm的直线 | |
| D. | 等腰△ABC的底边BC固定,顶点A的轨迹是线段BC的垂直平分线 |
3.若⊙A和⊙B外切,它们的半径分别为8cm和2cm,则圆心距AB为( )
| A. | 6cm | B. | 6cm或10cm | C. | 10cm | D. | 4cm或6cm |
10.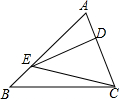 如图,在△ABC中,点D为AC上一点,点E为AB上一点,若AB=4,AD:DC=1:2且S△DEC=$\frac{1}{2}$S△ABC,则EB的长为( )
如图,在△ABC中,点D为AC上一点,点E为AB上一点,若AB=4,AD:DC=1:2且S△DEC=$\frac{1}{2}$S△ABC,则EB的长为( )
 如图,在△ABC中,点D为AC上一点,点E为AB上一点,若AB=4,AD:DC=1:2且S△DEC=$\frac{1}{2}$S△ABC,则EB的长为( )
如图,在△ABC中,点D为AC上一点,点E为AB上一点,若AB=4,AD:DC=1:2且S△DEC=$\frac{1}{2}$S△ABC,则EB的长为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
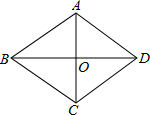 平行四边形ABCD的两条对角线相交于O,OA,OB,AB的长度分别为3cm、4cm、5cm,四边形ABCD是菱形吗?
平行四边形ABCD的两条对角线相交于O,OA,OB,AB的长度分别为3cm、4cm、5cm,四边形ABCD是菱形吗?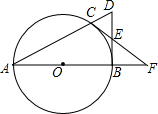 如图,点C是以AB为直径的圆O上一点,直线AC与过B点的切线相交于D,点E是BD的中点,直线CE交直线AB于点F.
如图,点C是以AB为直径的圆O上一点,直线AC与过B点的切线相交于D,点E是BD的中点,直线CE交直线AB于点F.