Question

6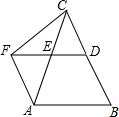．如图，在△ABC中，点D、E分别是边BC、AC的中点，过点A作AF∥BC，与DE的延长线相交于点F，连接CF．
（1）求证：四边形ABDF是平行四边形；
（2）若∠CAF=45°，BC=AC，直接写出图中（不添加其它线段）等于67.5°的所有角．

Answer 1

分析 （1）利用三角形中位线定理得出DE∥AB，进而利用平行四边形的判定方法得出即可；
（2）利用等腰三角形的性质以及平行线的性质分别得出等于67.5°的所有角．

解答 （1）证明：∵点D、E分别是边BC、AC的中点，
∴DE∥AB，
∵AF∥BC，
∴四边形ABDF是平行四边形；

（2）解：∵∠CAF=45°，AF∥BC，
∴∠ACB=45°，
∵BC=AC，
∴∠CAB=∠CBA=67.5°，
∵四边形ABDF是平行四边形，
∴∠AFD=67.5°，∠CDF=∠B=∠CED=∠FEA=67.5°，
故∠AEF=∠AFE=∠CED=∠CDE=∠CAB=∠CBA=67.5°．

点评 此题主要考查了平行四边形的判定与性质以及等腰三角形的性质等知识，熟练应用三角形的中位线定理得出DE∥AB是解题关键．