题目内容
11.在锐角△ABC中,AD是BC边上的高,DE⊥AB,DF⊥AC,E、F是垂足,求证:E、B、C、F四点共圆.分析 首先证明点AEDF四点共圆,从而可得到∠EAD=∠EFD,然后证明∠ADF=∠C,从而得到∠BEF+∠C=180°,从而可证四点共圆.
解答 解:如图所示:以AD为直径作圆,并连接EF.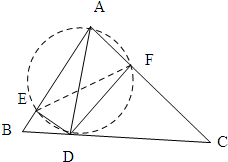
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
∴∠AED+∠AFD=180°.
∴A、E、D、F四点共圆.
∴∠AEF=∠ADF.
又∵∠DAF+∠ADF=90°,∠C+∠DAC=90°,
∴∠C=∠ADF.
∴∠C=∠AEF.
∵∠AEF+∠BEF=180°,
∴∠C+∠BEF=180°.
∴B、E、F、D四点共圆.
点评 本题主要考查的是四边共圆的条件和圆周角定理的应用,利用圆周角定理进行角的转化得到∠C=∠AEF是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知某几何体的三视图(单位:cm),则该几何体的侧面积等于( )cm2.


| A. | 12π | B. | 15π | C. | 24π | D. | 30π |
 (1)分别化简$4\sqrt{\frac{1}{2}}$,$\frac{2}{5}\sqrt{125}$;
(1)分别化简$4\sqrt{\frac{1}{2}}$,$\frac{2}{5}\sqrt{125}$; 如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC,与DE的延长线相交于点F,连接CF.
如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC,与DE的延长线相交于点F,连接CF. 如图,已知AB∥CD∥EF,∠ABC=46°,∠CEF=154°,求:
如图,已知AB∥CD∥EF,∠ABC=46°,∠CEF=154°,求: